Задание 5.1. Таблица 5.1. · Оцените тесноту связи между среднедушевым доходом и потреблением фруктов и ягод с помощью коэффициента корреляции и детерминации

Задание 5. 1

На основании имеющихся данных в табл. 5. 1:

· Методом приведения параллельных рядов, установите направление и характер связи между среднедушевым доходом и потреблением фруктов и ягод. Изобразите взаимосвязь графически в виде корреляционного поля

· Рассчитайте параметры линейного уравнения парной регрессии. Поясните смысл коэффициента регрессии. Определите теоретические (полученные по уравнению регрессии) значения потребления () и нанесите их на построенное корреляционное поле.  

· Оцените тесноту связи между среднедушевым доходом и потреблением фруктов и ягод с помощью коэффициента корреляции и детерминации. Рассчитайте коэффициент эластичности. Сделайте выводы по рассчитанным коэффициентам.

· Рассчитайте теоретическое корреляционное отношение (индекс корреляции).

· Оцените значимость:

· полученного уравнения регрессии с помощью критерия Фишера

· коэффициента корреляции с помощью критерия t при уровне значимости 0, 05.

 

Таблица 5. 1

Среднедушевой доход и потребление фруктов и ягод в РФ за 2010 г.

Среднедушевой доход, тыс. руб.
Среднедушевое потребление фруктов и ягод, кг.

Таблица 5. 2

Расчет параметров уравнения регрессии, коэффициента корреляции и корреляционного отношения

№группы	x	y	x2	y2	xy
Всего
В среднем						х	х	х	х	х

 

Задание 5. 2

Имеются следующие данные о выработке рабочих в зависимости от стажа (табл. 5. 3).

· С помощью дисперсионного анализа выявите зависимость между этими показателями. Установите существенность влияния факторов с помощью критерия Фишера. Результаты оформите в таблице 5. 4.

· Определите тесноту связи между стажем и выработкой с помощью эмпирического корреляционного отношения и шкалы Чеддока. Сделайте выводы.

Таблица 5. 3

Стаж работы и выработка

Исходные данные		Расчетные показатели
Стаж работы, лет	Выработка на 1 работника, дет. за смену	fi	Средние yгрi	Дгрi
До 3	7, 8, 6, 9, 10
4-10	12, 11, 10, 14, 15, 16
Свыше 10	14, 17, 18, 21, 24, 28, 30
Итого			x	x

 

Таблица 5. 4

Результаты дисперсионного анализа

Дисперсия	Значение дисперсии	Степень свободы	Девиация (дисперсия на одну степень свободы)	Критерий Фишера
				F факт	F табл
Межгрупповая
Внутригрупповая
Общая

 

 

Тема 6: Статистическое изучение динамики социально-экономических явлений

Динамический ряд представляет собой хронологическую последовательность числовых значений статистических показателей.

Ряд динамики состоит из 2 элементов:

1. ряд уровней, характеризующий величину явления (y_i)

ряд периодов или моментов времени (t_i).

По признаку времени ряды динамики могут быть: моментные и интервальные (с равными и неравными интервалами времени).

Показатели изменения уровней ряда:

1) абсолютный прирост -показывает, на сколько изменился изучаемый показатель по сравнению с предыдущим или базисным периодом времени

2) Коэффициент роста показывает, во сколько раз изменился изучаемый показатель по сравнению с предыдущим периодом времени или с базисным периодом времени

3) темпы роста (снижения)- это коэффициент роста, выраженный в %.,

4) темпы прироста (снижения)- показывает, на сколько процентов изменился изучаемый показатель;

5) абсолютное значение 1% прироста - характеризует весомость каждого процента прироста, т. е. показывает, сколько абсолютных единиц содержится в 1% прироста.

Средние характеристика ряда динамики

· средний уровень характеризует типическую величину абсолютных уровней.

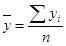Средний уровень интервального ряда с равными интервалами определяется по формуле средней арифметической простой:

 

В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:

 

 

В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:

 

где – продолжительность i-го интервала времени (интервал времени между двумя соседними значениями);

   - средний уровень ряда для i-го интервала времени

· Средний абсолютный прирост:

 

где m- количество абсолютных цепных приростов, причем их на 1 меньше, чем число периодов, т. е. m=n-1, т. к. у первого периода он не определяется.

· Средний коэффициент роста:

 

Методы выявления основной тенденции (тренда):

· Укрупнение интервалов:

· Скользящая средняя;

· Аналитическое выравнивание.

Процедура выравнивания в этом случае сводится:

· к выбору вида функции;

· к определению параметров функции;

· к получению выравненных значений уровней ряда на основе функции

Линейное уравнение тренда: ,

где а и в – параметры,

t – время

При применении способа отсчета он «условного нуля» при ∑ t=0 система уравнений примет вид:

 

 

 По полученному уравнению тренда можно сделать точечный прогноз, подставив в него номер (t) прогнозируемого года. Для интервального прогноза рассчитывается предельная ошибка по формуле:

 

 

где m- число параметров уравнения (при выравнивании по прямой -2: а и b)

t- коэффициент доверия, определяемый из статистических таблиц t-распределения Стьюдента в зависимости от уровня значимости и числа степеней свободы (ν =n-m)

 

Студент должен

знать:

· Виды рядов динамики;

· Основные показатели динамики;

уметь:

· Определять средний уровень ряда, основываясь на его виде;

· Рассчитывать и интерпретировать показатели динамики;

· Выявлять основную тенденцию ряда динамики;

· Делать прогнозы с учетом тенденции ряда.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: