 |
Рис. 2.2. Линии границ доверительных интервалов
|
|
|
|
Рис. 2. 2. Линии границ доверительных интервалов
2. 6. Доверительный интервал для индивидуальных
значений 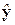
Выше мы построили доверительный интервал для СВ - условного среднего  (х). Случайной эта средняя величина является в силу того, что параметры регрессии b0 и b1 сами являются случайными величинами. Однако в каждой реализации
(х). Случайной эта средняя величина является в силу того, что параметры регрессии b0 и b1 сами являются случайными величинами. Однако в каждой реализации  (х) отклоняется от своего среднего, являясь, таким образом, как бы дважды случайной величиной. Ясно, что для индивидуальных значений
(х) отклоняется от своего среднего, являясь, таким образом, как бы дважды случайной величиной. Ясно, что для индивидуальных значений  (х) доверительный интервал будет еще больше, чем для средних значений
(х) доверительный интервал будет еще больше, чем для средних значений  (х).
(х).
На рис. 2. 2 этот доверительный интервал, также зависящий от х, представлен двумя тонкими плавно изогнутыми линиями. Именно этот интервал и определяет точность (конус) прогноза.
При определении доверительного интервала для индивидуальных значений  зависимой переменной нужно учесть ее рассеяние вокруг линии регрессии, т. е. в суммарную дисперсию
зависимой переменной нужно учесть ее рассеяние вокруг линии регрессии, т. е. в суммарную дисперсию  нужно включить еще s2. Тогда получим оценку дисперсии индивидуальных значений
нужно включить еще s2. Тогда получим оценку дисперсии индивидуальных значений  для данного х:
для данного х:
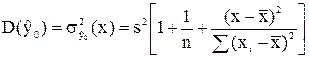 . .
| (2. 27) |
Искомый доверительный интервал для индивидуальных значений  :
:
 - t1-a, n-2 - t1-a, n-2 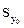 £ £  £ £  + t1-a, n-2 + t1-a, n-2 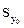 . .
| (2. 28) |
2. 7. Доверительный интервал для параметров регрессии
Иногда задача эконометрического исследования требует интервального оценивания параметров регрессии, в частности, для коэффициента регрессии b1 и дисперсии ошибки s2. Доказано, что при выполнении предпосылки-5 статистика t = (b1 -b1)/ /sb1 имеет стандартный НЗР, а статистика
 . .
| (2. 29) |
имеет t-распределение Стьюдента с k=n-2 степенями свободы. Поэтому доверительный интервал для b1 с доверительной вероятностью 1-a имеет вид:
|
|
|
 . .
| (2. 30) |
Построим доверительный интервал для s2. Статистика ns2 / s2 имеет распределение c2 с k=n-2 степенями свободы. Поэтому интервальная оценка с уровнем значимости a имеет вид:
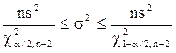 . .
| (2. 31) |
Доверительный интервал выбирается так, что:
Р(c2 <  ) = Р(c2 >
) = Р(c2 >  ).
).
2. 8. Оценка значимости уравнения регрессии
Оценить значимость регрессии - значит подтвердить или опровергнуть суждение о том, что математическая модель, выражающая связь между переменными, соответствует наблюденным данным и что для описания зависимой переменной достаточно объясняющих переменных.
Для решения задачи используются элементы дисперсионного анализа, согласно которому:
| Q = QR + Qe, | (2. 32) |
где Q = å (yi -  )2 - общая сумма квадратов отклонений зависимой переменной от ее средней; QR = å (
)2 - общая сумма квадратов отклонений зависимой переменной от ее средней; QR = å (  -
-  -)2 - сумма квадратов отклонений, обусловленная регрессией; Qe = å (yi -
-)2 - сумма квадратов отклонений, обусловленная регрессией; Qe = å (yi -  )2 - остаточная сумма квадратов отклонений, обусловленная влиянием неучтенных факторов. Схема дисперсионного анализа отражена в табл. 2. 4.
)2 - остаточная сумма квадратов отклонений, обусловленная влиянием неучтенных факторов. Схема дисперсионного анализа отражена в табл. 2. 4.
Таблица 2. 4
Схема дисперсионного анализа
| Вид дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты (дисперсии) |
| Регрессия | QR = å (  - -  2 2
| m-1 |  = QR / (m-1) = QR / (m-1)
|
| Остаточная | Qe = å (  - -  )2 )2
| n-m | s2 = Qe / (n-m) |
| Общая | Q = å (  - -  )2 )2
| n-1 |
Примечание: в графе 4 средние квадраты являются несмещенными оценками соответствующих дисперсиий.
Из схемы дисперсионного анализа: уравнение регрессии будет значимо на уровне a, если фактическое значение статистики F больше его табличного значения (отвергаем нулевую гипотезу Но о незначимости регрессии и принимаем конкурирующую с ней гипотезу Н1 о значимости):
 , ,
| (2. 33) |
где Fa, k1, k2 - табличное (критическое) значение F-критерия Фишера-Снедекора для уровня значимости a, степеней свободы k1 = m-1, k2 = n-m.
|
|
|
Смысл статистики F прозрачен: его значение показывает, во сколько раз объясненная регрессией дисперсия  СВ
СВ  больше остаточной (необъясненной) дисперсии s2 СВ е. Чем больше это отношение, тем более значимо уравнение регрессии.
больше остаточной (необъясненной) дисперсии s2 СВ е. Чем больше это отношение, тем более значимо уравнение регрессии.
Для парной регрессии m=2 и критерий Фишера-Снедекора формулируется так:
уравнение значимо, если  . .
| (2. 34) |
Значимость уравнения парной регрессии можно равносильно оценить и иначе, по коэффициенту регрессии b1. Действительно, если нулевая гипотеза Но состоит в том, что b1 незначимо отличается от 0, и она подтверждается, то прямая регрессии расположена параллельно оси ОХ: объясняющая переменная Х ничего не объясняет. И наоборот: если b1 значимо отличается от 0, значит и все уравнение парной регрессии значимо.
Соответствующий критерий на основе статистики Стьюдента:
Но: b1=0 отвергается, если ç t ç = ç 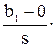  ç > t1-a, n-2. ç > t1-a, n-2.
| (2. 35) |
Равносильность критериев для парной регрессии вытекает из их функциональной связи: F=t2.
Иногда эконометристу требуется оценить значимость коэффициента корреляции. Соответствующий критерий:
Но: r=0 отвергается, если ç t ç =ç r ç  > t1-a, n-2. > t1-a, n-2.
| (2. 36) |
В теории и практике эконометрики используется еще один критерий качества регрессионной модели - коэффициент детерминации:
| R2 = QR/Q = 1 - Qe/Q. | (2. 37) |
Очевидно, что 0£ QR£ Q. Отсюда свойство коэффициента детерминации: 0 £ R2 £ 1. Значение R2 показывает, какую долю составляет вариация регрессионной переменной по отношению к общей вариации объясняемой переменной. Ясно, что чем ближе R2 к 1, тем регрессионная модель более адекватна, имеет большую прогностическую силу, лучше подходит к наблюденным данным.
Критерий значимости уравнения регрессии (2. 33) можно эквивалентно записать с помощью коэффициента детерминации:
F = 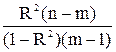 > Fa, k1, k2. > Fa, k1, k2.
| (2. 38) |
Для парной регрессии коэффициент детерминации равен квадрату коэффициента корреляции: R2 = r2.
|
|
|


