 |
Рис. 1.2. Эконометрическая модель связи потребления Y и дохода X
|
|
|
|
Рис. 1. 2. Эконометрическая модель связи потребления Y и дохода X
Для предметов 1-й необходимости (питание, одежда, жилье и пр):
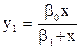 . .
| (1. 2) |
Некоторые свойства функции у1, которые отражают смысл явления:
- при доходе х, близком к нулю, у1 идет вдоль биссектрисы: все доходы расходуются на предметы первой необходимости: у1»х,
- при заметном росте доходов х потребление у1 асимптотически приближается к пределу: у1 =bо .
Для предметов средней необходимости (газеты, пылесос, стиральная машина и пр):
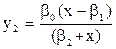 . .
| (1. 3) |
Свойства функции у2:
- расходы на предметы средней необходимости начинаются (у2> 0) при уровне доходов х > b1, поэтому у2 (и у3 по этой же причине) требует доопределения;
- при значительном росте доходов х потребление у2 асимптотически приближается к тому же пределу у2 =bо;
- из второго свойства вытекает: пределы расходов на предметы первой и средней необходимости равны между собой (это частный случай конкретной экономики).
Для предметов роскоши (предметы искусства, драгоценности, престижный дом и пр. ):
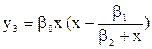 . .
| (1. 4) |
Свойство функции у3:
- расходы у3 на предметы роскоши при неограниченном увеличении доходов х также неограниченно увеличиваются.
Теперь заметим, что если доходы х расходуются только на цели у1, у2, у3, то сумма последних должна в точности быть равной доходам. Так мы приходим к 4-й - совместной - функции в исследуемой эконометрической модели (см. подробнее параграф 1. 3: системы совместных уравнений):
| у1(х)+ у2(х) +у3 (х) = х. | (1. 5) |
1. 2. Данные наблюдений для эконометрического моделирования
Для построения эконометрической модели используется выборка значений зависимой переменной Y и выборки по каждой из объясняющих переменных X1, X2, ... , Xp. Число наблюдений n должно примерно на порядок и больше превышать число объясняющих переменных р и быть достаточно велико. Например, р=2 - две объясняющие переменные и n=22 – число наблюдений.
|
|
|
Увеличению n препятствует либо ограниченный объем данных наблюдения, либо неоднородный состав этих данных и необходимость разбивать их на однородные массивы (кризисы в экономике, резкие изменение конъюнктуры рынка и т. п. ).
Другая проблема - необходимость делать предположение о том, что условное распределение СВ Y одинаково при различных наборах значений объясняющих переменных Х.
Исходные данные делят на два типа: пространственные и временные. Под пространственными данными понимаются результаты наблюдений по множеству объектов за одинаковый интервал или на один момент времени, например, выборка рентабельности по n средним и большим предприятиям города за 2004 г. Важно то, что порядок изучения предприятий и расположения их в выборке здесь не имеет значения.
Формально пространственной выборкой называют серию из n независимых наблюдений (р+1)-мерной СВ (X1, X2, ... , Xp, Y). При этом различные СВ Yi обычно принимаются независимыми и отсюда следует некоррелированность возмущений:
| r(ei, ej) = 0 при i¹ j. | (1. 6) |
Это условие упрощает модель и ее анализ. Однако практически доказать независимость случайных величин часто оказывается невозможным, поскольку есть доводы как за, так и против этой гипотезы. Например, довод против независимости: все наблюдаемые предприятия находятся в однородной рыночной среде (курсы валют, законодательная база, цены на мировом рынке и пр. ).
Таким образом, эконометрическая модель на основе пространственных наблюденных данных (xi, yj) имеет вид:
| yi=f(xi) + ei, i=1, 2, ... , n. | (1. 7) |
|
|
|
Ошибки регрессии удовлетворяют условиям:
| - математическое ожидание ошибок наблюдений М(ei, )=0; | (1. 8) |
| - коэффициент корреляции между ошибками наблюдений r(ei, ej)=0; | (1. 9) |
| - дисперсия ошибок наблюдений D(ei)=si2. | (1. 10) |
Дисперсия ошибок (1. 10) может быть двух типов:
а) одинаковой для всех наблюдений: si2 = sj2 при всех i и j. Постоянство дисперсий ошибок называется гомоскедастичностью, это свойство облегчает проведение анализа модели;
б) неодинаковой для различных наблюдений: si2 ¹ sj2 . Это свойство дисперсий называется гетероскедастичностью. Оно затрудняет статистический анализ и может потребовать ее устранения.
Временной выборкой (временным рядом) называется такая выборка, в которой нельзя без потери смысла произвольно менять порядок следования наблюденных значений: каждое значение связано с определенным моментом времени. Обычно предполагается, что в разные моменты времени тип распределения наблюдаемой СВ остается одним и тем же, хотя параметры распределения меняются во времени. Очень часто при этом близко расположенные по времени значения СВ не являются независимыми. Отсюда следует коррелированность ошибок между собой. Это значительно усложняет анализ модели.
|
|
|


