Условные данные по субъектам России за 199Хг.

Условные данные по субъектам России за 199Хг.

Субъект РФ	Y	X
Субъект-1	68, 8	45, 1
Субъект-2	61, 2	59, 0
Субъект-3	59, 9	57, 2
Субъект-4	56, 7	61, 8
Субъект-5	55, 0	58, 8
Субъект-6	54, 3	47, 2
Субъект-7	49, 3	55, 2

Расчеты удобно проводить с использованием таблицы типа табл. 2. 2.

 

Таблица 2. 2  

Промежуточные расчетные данные

№ п/п	уi	xi	уi xi				yi -
	68, 8	45, 1	3102, 88	2034, 01	4733, 44	61, 3	7, 5
	61, 2	59, 0	3610, 80	3481, 00	3745, 44	56, 5	4, 7
	59, 9	57, 2	3426, 28	3271, 84	3588, 01	57, 1	2, 8
	56, 7	61, 8	3504, 06	3819, 24	3214, 89	55, 5	1, 2
	55, 0	58, 8	3234, 00	3457, 44	3025, 00	56, 5	-1, 5
	54, 3	47, 2	2562, 96	2227, 84	2948, 49	60, 5	-6, 2
	49, 3	55, 2	2721, 36	3047, 04	2430, 49	57, 8	-8, 5
Итого	405, 2	384, 3	22162, 34	21338, 41	23685, 76	405, 2	0, 0
Средн.	57, 89	54, 90	3166, 05	3048, 34	3383, 68	-	-
s	5, 74	5, 86

         

Решение. В табл. 2. 2 графы 2 и 3 - наблюденные пары значений переменных Y и Х, графы 4-6 вычисляются непосредственно на основе граф 2 и 3. Остальные графы в этом примере не используются.

     По формулам (2. 7) рассчитаем параметры регрессии b₀ и b₁, получим искомое уравнение регрессии:

 

= 76, 88 - 0, 35x.

(2. 10)

         

Смысл параметра уравнения b₁: при увеличении среднесуточного дохода на 1 руб. расход на продовольствие сократится на 0, 35% от общей суммы среднесуточного расхода. Свободный член b₀ смысла не имеет.

    

2. 2. Связь коэффициентов регрессии и корреляции

 

Если значение b_o из формул (2. 7) подставить в уравнение регрессии (2. 2)_, то после преобразований получим уравнение регрессии в отклонениях (прямая проходит через начало координат - точку ( )).

     Преобразуем это уравнение: разделим обе части на s_y, умножим и разделим правую часть на s_x, получим:

 

.

 

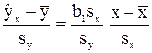где коэффициент  r = b1 sx/sy показывает, на сколько величин sy  изменится в среднем Y, если Х увеличится на одно значение sx.

(2. 11)

     Другой вариант формулы для расчета r:

 

.

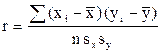(2. 12)

 

     Статистика r - выборочный коэффициент корреляции - отражает тесноту статистической связи случайных величин Х и Y. Свойства коэффициента корреляции (рис. 2. 1):

1. -1 £ r £ 1. Чем ближе модуль ç r ç к 1, тем теснее связь Х и Y.

2. Если r = ± 1, то связь между Х и Y - функциональная и линейная.

3. Если r = 0, то линейная корреляционная связь между СВ Х и Y отсутствует.

4. Коэффициент r является непосредственной оценкой генерального коэффициента корреляции r между Х и Y лишь в случае двухмерного НЗР случайной величины (Х, У). В других случаях r не является строгой мерой взаимосвязи переменных.

               

у                                                         у                                                    у

           r = +1                                               r » +0, 8                                          r » +0, 5

 

 

                                               х                                                       х                                                  х

                        а)                                                      б)                                                  в)

 

 

   у r = -1                                  у             r » -0, 8                      у             r » -0, 5

 

 

                                                х                                                       х                                                 х

                          г)                                                     д)                                                е)

 

 

Рис. 2. 1. Примеры полей корреляции и значений r

 

           Пример 2. 2.  По данным табл. 2. 1 и примера 2. 1 рассчитать значение коэффициента корреляции r. Для расчета используем формулу (2. 11): r = b₁ s_x / s_y. Неизвестные СКО s_x и s_y  рассчитаем по формулам и данным табл. 2. 1:

.

 

.

 

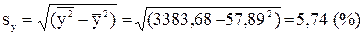Окончательно: r = b₁ s_x / s_y = -0, 35× 5. 86 / 5, 74 = -0, 36.

Данное значение r характеризует связь между Х и Y как умеренную и обратную (см. рис. 2. 1. е).

 

2. 3. Основные положения регрессионного анализа

 

     Напомним, что парная регрессионная модель представляется в виде:

 

Y = j(Х) + e,

(2. 13)

где e - СВ - возмущение, ошибка, характеризующая отклонение СВ Y от функции регрессии j(Х) - условного математического ожидания М_х(Y). В линейном регрессионном анализе j(Х) линейна относительно оцениваемых параметров:

 

Мх(У) = j(Х) = b0 +b1х.

(2. 14)

         

Пусть для оценки параметров регрессии взята выборка из n пар (x_i, y_i). Тогда линейная парная регрессионная модель имеет вид:

 

yi = b0 +b1хi + ei.

(2. 15)

         

Теперь рассмотрим основные предпосылки регрессионного анализа:

1. В модели (2. 15) возмущение e_i , а значит и зависимая переменная y_i, есть величина случайная, а объясняющая переменная х_i - величина неслучайная, но принимающая различные значения.

 

2. М(ei) = 0 и, следовательно, М(yi) = b0 +b1хi.

(2. 16)

 

3. Условие гомоскедастичности (равноизменчивости) возмущения или, что то же самое, переменной yi:

 

D(ei) = s2 = D(yi) = const.

(2. 17)

 

4. Возмущения e_i и e_j (или переменные у _i и у _j) некоррелированы:

М(eiej) = 0 (i¹ j).

(2. 18)

5. Возмущение e_i (или переменная у_i) есть НРСВ.

     Модель, для которой выполняются все пять предпосылок, называется нормальной классической линейной регрессионной моделью (НКЛРМ). Для получения уравнения регрессии достаточно предпосылок 1-4. Предпосылка 5 необходима для оценки точности уравнения и его параметров.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: