 |
Рис. 6.3. Схема теста Дарбина-Уотсона
|
|
|
|
Рис. 6. 3. Схема теста Дарбина-Уотсона
Недостатки теста Дарбина-Уотсона: наличие зон неопределенности критерия, ограниченность результата - выявление корреляции только между двумя соседними членами ряда.
Тест Бреуша-Годфри основан на выражении корреляции между соседними наблюдениями авторегрессионным уравнением первого порядка:
| et = rе t-1 , t=1, 2, ... , n, | (6. 21) |
где et - остатки регрессии, полученные обычным МНК.
Тест состоит в следующем: если коэффициент регрессии r значимо отличается от нуля, то автокорреляция имеет место.
Преимущества этого теста перед тестом Дарбина-Уотсона:
- не содержит зон неопределенностей;
- может измерять наличие автокорреляции не только между смежной парой возмущений, но и с учетом других возмущений: е t-2 , е t-3 . Для этого в уравнение (6. 21) нужно ввести эти регрессоры.
Существуют и другие тесты.
6. 7. Идентификация временного ряда и устранение автокорреляции
Основная причина автокорреляции ошибок - наличие скрытых регрессоров. Их влияние и проявляется через случайную составляющую. Это говорит о низком качестве отбора значимых факторов на начальном этапе построения регрессионной модели и выборе самой модели. Все это называется идентификацией модели или временного ряда.
Очень часто скрытыми факторами являются лаговые объясняемые переменные yt-1, yt-2 и т. д. Действительно, если мы строим прогнозное уравнение регрессии курса валют, то именно эти лаговые переменные включим в уравнение в качестве объясняющих переменных в первую очередь. Другой класс объясняющих переменных - макропоказатели экономики: цена на нефть на мировом рынке, индексы активности экономики России и других стран, уровень политической (военной) напряженности в наиболее горячей точке планеты и т. п.
|
|
|
Таким образом, автокорреляция устраняется, если мы качественно выполним идентификацию временного ряда, т. е. построим модель такую, в которой остатки представляют собой " белый шум", а все регрессоры значимы.
Такая модель не единственна, поэтому выбирают самую простую из трех типов: авторегрессионную модель р-го порядка АR(p), модель скользящей средней q-го порядка MA(q) и авторегрессионную модель скользящей средней ARMA(p, q).
Авторегрессионная AR(p) модель (см. уравнение (5. 8)) имеет вид:
| yt=bо+ b1 yt-1+ b2 yt-2 +... + bр yt-р + et ; t=1, 2, ... , n. | (6. 22) |
Модель скользящей средней MA(q):
| yt=et+ g1et-1+ g2 et-2 +... + gqet-q ; t=1, 2, ... , n. | (6. 23) |
Авторегрессионная модель скользящей средней ARMA(p, q):
| yt=bо+ b1 yt-1+ b2 yt-2 +... + bр yt-р +et+ g1et-1+... + gqet-q t=1, 2, ... , n | (6. 24) |
Чаще всего на практике используется метод проб и ошибок: проверяются на пригодность различные модели, начиная с самых простых.
В качестве ориентира для идентификации можно использовать автокорреляционую и частную автокорреляционую функции. Если все значения r(t) порядка выше q близки к нулю, то применяется модель МА с порядком не выше q. Например, из рис. 5. 1 видно, что можно принять q»2.
Если все значения частной автокорреляционной функции порядка выше р близки к нулю, то применяется модель AR с порядком авторегрессии не выше р. В конечном счете мы и получим модель без авторегрессии.
В качестве примера рассмотрим авторегресионную модель 1-го порядка. Пусть мы имеем регрессионную модель
| Y=Xb+e или yt =b0 + å bixtj +et t=1, ... , n | (6. 25) |
и пусть возмущения связаны наиболее просто – авторегрессионным процессом 1-го порядка:
| et = ret-1+nt, | (6. 26) |
|
|
|
где nt - " белый шум" (М(nt)=0 и D(nt)=s02) и r - коэффициент авторегрессии.
Отсюда из выражения (6. 26) нетрудно получить формулу:
s2 = 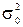 /(1-r2) /(1-r2)
| (6. 27) |
и далее для коэффициентов автокорреляции 1-го и m-го порядков:
| r(et, et-1) = r и r(et, et-m) = rm. | (6. 28) |
На основе формул (6. 27) и (6. 28) можно записать ковариационную матрицу вектора возмущений e:
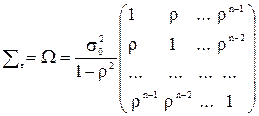 . .
| (6. 29) |
Для получения наиболее эффективных значений параметра b применяется обобщенный МНК. Неизвестное значение r оценивается применением к регрессии (6. 26) обычного МНК.
Можно пойти другим путем. Исключая et из уравнений (6. 25) и (6. 26), получим классическую ЛММР: возмущения nt независимы и имеют постоянную дисперсию 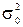 :
:
| yt - ryt-1 =b0(1-r) + å bj(xtj - rxt-1j)+n t t=1, ... , n. | (6. 30) |
Таким образом, автокорреляция легко устраняется.
|
|
|


