 |
Вопросы для самопроверки. 7. Регрессионные динамические модели. 7.1. Последствия и причины стохастичности регрессоров. 7.2. Устранение коррелированности регрессоров и ошибок методом инструментальных переменных
|
|
|
|
Вопросы для самопроверки
1. Как может выглядеть произвольная числовая матрица å b для р=2?
2. Как может выглядеть произвольная числовая матрица W для n=3?
3. В чем различие между классической линейной моделью и обобщенной?
4. Почему так важно получить метод оценивания с минимальной дисперсией?
5. Раскройте смысл теоремы Айткена.
6. Каким образом мы приходим к образу Y* обобщенной модели и что это нам дает?
7. Как формулируется критерий оптимальности (минимум суммы квадратов отклонений) в обобщенном МНК?
8. Какие практические сложности возникают в использовании обобщенного МНК и как предлагается их преодолеть?
9. Как отражается гетероскедастичность на свойствах вектора оценок b?
10. В чем суть теста ранговой корреляции Спирмена?
11. В чем суть теста Голдфелда-Квандта?
12. В чем суть теста Уайта?
13. С какой целью вводятся новые переменные (нормированные через СКО) и соответствующее уравнение регрессии (оно гомоскедастично)?
14. Почему метод наименьших квадратов называется взвешенным?
15. К каким последствиям приведет применение МНК при наличии автокорреляции?
16. В чем суть теста Бреуша-Годфри?
17. Позволяет ли знание ковариационной матрицы (6. 29) применить к модели (6. 25) обобщенный МНК?
18. Можно ли после устранения автокорреляции применить к полученной модели обычный МНК для получения оценок ее качества?
7. Регрессионные динамические модели
7. 1. Последствия и причины стохастичности регрессоров
Ранее почти всегда предполагалось, что объясняющие переменные Xj (j=1, 2, ..., p) - регрессоры - являются детерминированными. Это обычно имеет место для пространственных выборок, но не тогда, когда присутствуют регрессоры, значения которых образуют временные ряды. И здесь важным является степень коррелированности регрессоров с ошибками регрессии e. Будем предполагать, что Хt и Yt - стационарные временные ряды.
|
|
|
Рассмотрим три случая.
1. Регрессоры Х и ошибки регрессии e не коррелируют. Это значит, что генеральная ковариация Cov(xs, et)=0 для всех s, t=1, 2, ..., n. В этом случае оценка b является несмещенной и состоятельной.
2. Регрессоры Х не коррелируют с ошибками e в данный момент t, но коррелируют в более ранние моменты времени t-1, t-2... . В этом случае оценка b перестает быть несмещенной, но остается состоятельной.
3. Регрессоры Xt коррелированы с ошибками et в том числе в одинаковые моменты времени. Оценка b в этом случае будет смещенной и несостоятельной.
Таким образом, коррелированность регрессоров и ошибок приводит к значительно более неприятным последствиям, чем гетероскедастичность или автокорреляция. Неадекватными являются как сами оценочные значения параметров, так и результаты тестирования гипотез - исследования качества уравнения регрессии.
Существуют две основных причины коррелированности регрессоров и ошибок. Первая причина - на ошибку e воздействуют те же факторы, что и на сами регрессоры. Воздействие на ошибку осуществляется через воздействие на результирующую переменную Y. Например, пусть в парной регрессии Х - себестоимость перевозки в расчете на тонно-километр, а Y - цена перевозки в руб. /т-км. Очевидно, что на себестоимость Х и цену Y будут одинаково влиять протяженность маршрута, состояние дорог и т. п. Вторая причина коррелированности регрессоров и ошибок - случайные ошибки при измерении Х.
Ниже рассмотрены методы исключения коррелированности регрессоров и ошибок.
7. 2. Устранение коррелированности регрессоров и ошибок методом инструментальных переменных
|
|
|
Суть метода состоит в подборе новых – инструментальных – переменных Zj (j=1, 2, …, h), которые тесно коррелируют с Xj и не коррелируют с e. Обычно количество инструментальных переменных Z не меньше, чем количество исходных переменных X. Соответствующая оценка параметров регрессии будет состоятельной:
| b Z=(Z’X)-1Z’Y=(Z’X/n)-1(Z’Y/n), | (7. 1) |
где X, Y, Z – матрицы значений наблюденных переменных.
Для уравнения парной регрессии формула (7. 1) примет вид:
 .
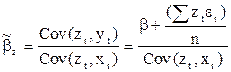| (7. 2) |
Очевидно, что при n®¥ по вероятности b Z®b, что и означает состоятельность оценок (7. 1) и (7. 2), но отсюда не следует их несмещенность, не говоря уже об эффективности – минимальной ковариации.
Как находить нужные инструментальные переменные? В работе [6, с. 181] отмечается: " Дать строгий однозначный ответ … невозможно. Все зависит от конкретной ситуации. Может так случиться, что инструментальных переменных нельзя найти, а может быть, что существует и несколько таких инструментов".
Например, если изучается зависимость Y – среднедушевых расходов семей на определенный товар (руб. /чел. -мес. ) от ненаблюдаемой переменной X – истинного среднедушевого дохода семей (руб. /чел. -мес. ), то в качестве инструментальной переменной можно взять Z – размер объявленного среднедушевого дохода семьи (руб. /чел. -мес. ).
Практическая реализация метода инструметальных переменных приводит нас к двухшаговому методу наименьших квадратов:
- сначала осуществляется регрессия Х на Z и находятся прогнозные значения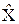 
, они теперь и будут считаться новыми независимыми переменными;
- искомая оценка вектора параметров b строится с помощью обычной регрессии Y на .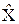
Таким образом, в двухшаговом МНК собственно МНК применяется дважды: сначала для построения регрессоров 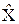, а затем для нахождении оценки b.
В заключение заметим, что вопрос о необходимости использования инструментальных переменных решается в форме проверки статистической гипотезы. Соответствующая процедура носит название теста Хаусмана.
|
|
|
