1.5. Двумерный нормальный закон распределения

Рис. 1. 3

 

Свойства условного МО:

1. Если Z = z(X), где z - неслучайная функция от Х, то M_z(M_x(Y)) = =M_z(Y), в частности, М(М_х(Y)) = М(У).

2. Если Z = z(X), то M_z(Z× Y) - Z× М_х(Y).

3. Если СВ Х и Y независимы, то М_х(Y) = М(Y) (на рис. 1. 3 это была бы горизонтальная прямая).

     Для независимых СВ j(x, y) = j₁(x)∙ j₂(y), или j_у(x) = j₁(x) и j_х(y) = j₂(y), где j₁ и j₂ - плотности одномерных СВ Х и Y, j_у(x) и j_х(y) - плотности условных распределений Х по Y и Y по Х.

     Зависимость между двумя СВ называется статистической, если каждому значению одной из них соответствует определенное (условное) распределение другой.

     Ковариацией (корреляционным моментом) Cov(Х, Y) СВ Х и Y называется МО произведения отклонений этих величин от своих МО:

 

Cov(Х, Y) = М((Х-ах)( Y-ау)).

(1. 26)

 

Другие обозначения ковариации: К_{ху, .}

     Ковариация двух СВ характеризует, во-первых, степень их взаимозависимости, во-вторых, их рассеяние вокруг точки (а_х, а_у).

     Для измерения только тесноты связи двух СВ применяют безразмерный коэффициент корреляции r:

 

r = Cov(Х, Y) / (sхsу).

(1. 27)

         

Свойства ковариации:

1. Cov(Х, Y) = 0, если Х и Y независимы.

2. Cov(Х, Y) = М(Х, Y) - а_х а_у.

3. ê Cov(Х, Y)ê £ s_хs_у.

     Свойства коэффициента корреляции r:

1. -1 £ r £ 1.

2. r = 0, если СВ Х и Y независимы. Обратное утверждение неверно.

3. если ê r ê = 1, то СВ Х и Y связаны линейной функциональной зависимостью.

 

1. 5. Двумерный нормальный закон распределения

 

     СВ (Х, Y) распределена по двухмерному нормальному закону распределения, если ее совместная плотность имеет вид:

jN(x, y) = 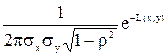,	(1. 28)
где  L(x, y) = 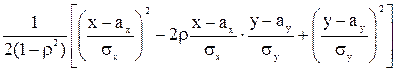.	(1. 29)

 

Здесь пять числовых характеристик: М(Х) = а_х , М(Y) = а_у, D(Х) = s_х², D(Y) =s_у², r_ху = r.

     Одномерные ЗР этих же СВ Х и Y также нормальные: N(a_х, s_х²), N(a_y, s_y²). Нормальными являются и условные ЗР Х по Y и Y по Х с числовыми характеристиками:

 

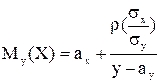
	(1. 30)
Dу(Х) = sх2(1-r2),	(1. 31)
	(1. 32)
Dx(Y) = sy2(1-r2).	(1. 33)

 

     Как видно из уравнений (1. 30) и (1. 32), регрессии М_у(Х), М_x(Y) нормально распределенных СВ являются прямыми линиями. Отсюда ясно, что для НР СВ из некоррелированности следует их независимость (при r=0 параметры условных ЗР, а значит и сами условные распределения, не зависят от смежной переменной из пары (Х, Y)).

     Двумерный НЗР обобщается на р-мерный для СВ Х=(Х₁, Х₂, ... , Х_р). Он характеризуется вектором математических ожиданий а=(а₁, а₂, ... , а_р) и ковариационной матрицей å _х = (s_ij)_рxр, где s_ij =М((Х_i-a_i)(X_j-a_j)) – смешанный момент второго порядка – аналог дисперсии одномерной случайной величины.

 

1. 6. Закон больших чисел и предельные теоремы

 

     Под законом больших чисел в широком смысле понимается следующее установленное свойство: совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Этот закон раскрывается в форме нескольких теорем.

     Теорема Чебышева. Если дисперсии n независимых СВ X₁, X₂, ... , X_n ограничены одной и той же постоянной, то при n®¥ средняя арифметическая случайной величины сходится по вероятности к средней арифметической их МО а₁, а₂, ... , а_n:

 

lim P( ê å Xi/n - å ai/n ê ) = 1 при n®¥.

(1. 34)

          

Частота события в n повторных независимых испытаниях, в каждом из которых оно может произойти с вероятностью р, при n®¥ сходится по вероятности к вероятности р этого события в отдельном испытании:

 

lim P( ê m/n - p ê £ e) = 1 при n®¥.

(1. 35)

 

           Теорема Ляпунова. Если независимые СВ Х₁, Х₂, ... , Х_n имеют конечные МО и дисперсии, при этом ни одна из этих характеристик резко не выделяется среди остальных, то при n®¥ ЗР их суммы å X_i  неограниченно приближается к нормальному.

 

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: