1.8. Проверка статистических гипотез

1. 8. Проверка статистических гипотез

 

           Статистической гипотезой называется любое предположение о свойстве параметра или неизвестного закона распределения. При этом возможны четыре исхода относительно основной - нулевой - гипотезы Н_о, (табл. 1. 2). Вероятность a допустить ошибку 1-го рода называется уровнем значимости критерия.

Таблица 1. 2

Гипотеза Но	Н0 принимается	Н0 отвергается
Но верна	Правильное решение	Ошибка 1-го рода (вероятность a) – уровень значимости критерия
Но неверна	Ошибка 2-го рода (вероятность b)	Правильное решение: вероятность 1-b есть мощность критерия

         

Суть проверки гипотезы состоит в том, что используется статистика , полученная по выборке x₁, x₂, ... , x_n . Затем по таблице определяется критическое значение Q_кр такое, что если гипотеза Н_о верна, то вероятность Р( > Q_кр) пренебрежимо мала. Поэтому, если обнаружится, что > Q_кр, то Н_о отвергается. Если же £ Q_кр, то гипотеза Н_о принимается.

     Вероятность 1-b не допустить ошибку 2-го рода называется мощностью критерия.

В зависимости от вида конкурирующей гипотезы Н₁ (она является отрицанием гипотезы Н_о ) выбирают правостороннюю, левостороннюю или двустороннюю критическую область. Границы критической области при заданном a определяются из соотношений:

· для правосторонней критической области:

 

Р(   > Qкр) = a,

(1. 40)

 

· для левосторонней критической области:

 

Р(   < Qкр) =a,

(1. 41)

 

· для двусторонней критической области:

 

Р(   < Qкр. 1) = Р(   > Qкр. 2) = a/2.

(1. 42)

 

     Проверка статистической гипотезы не дает логического (дедуктивного) доказательства ее истинности или ложности. Принятие гипотезы Н_о является лишь правдоподобным, не противоречащим опыту утверждением – индуктивным доказательством.

 

Приложение 2

Элементы матричной алгебры

 

     Матрицей называется прямоугольная таблица чисел (иногда – переменных или функций). С помощью матриц удобно проводить алгебраические преобразования и представлять полученные результаты.

Пример.  Пусть дана система двух уравнений с двумя неизвестными:

 

(2. 1)

 

Эту систему уравнений можно записать в матричной форме:

 

(2. 2)

 

В форме алгебраического матричного уравнения подобные системы будут иметь одинаковый вид:

АХ=В,

(2. 3)

где

	- квадратная матрица коэффициентов размера 2х2;
	- матрица-столбец искомых неизвестных размера 2х1;
	- матрица-столбец правых частей уравнений размера 2х1.

 

     Операции над матрицами. Матрицы можно суммировать, вычитать, умножать либо делить на скаляр. Делается это просто - почленно. Результатом будет матрица того же размера.

 

     Пример 2. 1. Суммирование двух матриц:

 

 

     Пример 2. 2. Умножение матрицы на скаляр:

 

 

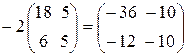
Сложнее операция перемножения двух матриц. Различают умножение слева и справа, поскольку эта операция некоммутативна. Перемножаемые матрицы должны иметь соответствующие размеры (1-й индекс - число строк, 2-й - число столбцов): А_m1xn1B_n1xn2 = C_m1xn2. При перемножении матриц повторяется одна и та же операция: очередная строка левой матрицы скалярно умножается на каждый столбец правой матрицы.

         

Пример 2. 3. Перемножение двух квадратных матриц:

 

         

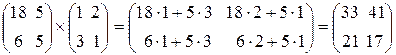
Операция транспонирования матрицы (обозначается штрихом или верхним индексом ^т) состоит в повороте матрицы на 90 градусов: 1-я строка становится 1-м столбцом, 2-я строка становится 2-м столбцом и т. д.

 

     Пример 2. 4. Транспонирование матрицы:

 

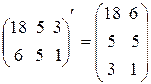
(2. 4)

 

     Операция обращения матрицы является самой сложной, включающей в себя много понятий и операций. Аналогом обратной матрицы в арифметике является обратное число по отношению к данному. Например, дано число 9. Обратным ему будет число 9^-1 =1/9.

Проверка: 9× 9^-1 = 9^-1 9=1. Аналогом единицы в матричной алгебре является квадратная единичная матрица Е, имеющая всюду нули, а на главной диагонали - единицы.

     Очевидно,  что  АЕ=ЕА=А. Из  определения  следует  также,  что АА^-1=А^-1А =Е. Обращению подлежат, во-первых, только квадратные матрицы, а во-вторых, неособенные, т. е. такие, определитель которых не равен нулю. Заметим, что в арифметике число 0 является особенным, поскольку не имеет обратного числа.

Формула обращения матрицы А:

 

А-1 =(1/ç А ç )(Аij)’,

(2. 5)

 

где ç А ç - определитель матрицы А,

(А_ij)’ - транспонированная матрица, составленная из алгебраических дополнений матрицы А.

Примечание: алгебраическим дополнением называется минор, взятый со своим знаком. Минор для ij-элемента матрицы находится как определитель подматрицы, получаемой из данной матрицы путем вычеркивания из нее i-й строки и j-го столбца.

     Пример 2. 5. Для исходной матрицы А найти матрицу алгебраических дополнений (А_ij):

 

(2. 6)

Пример 2. 6. Найти определитель матрицы А из примера 2. 5.

Решение. Определитель имеет третий порядок. Его можно вычислить непосредственно, а можно - путем разложения на определители второго порядка. Выберем второй подход:

 

.

 

Поскольку определитель ç А ç отличен от нуля, то матрица А неособенная и, следовательно, имеет обратную матрицу.

    

Пример 2. 7. Для матрицы А из предыдущего примера найти обратную матрицу А^-1:

(2. 7)

 

     Пример 2. 8. Проверить равенство АА^-1 =Е:

 

(2. 8)

 

В результате проверки получена единичная матрица Е, что и следовало ожидать.

 

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: