 |
6) Деформация при растяжении-сжатии
|
|
|
|
6) Деформация при растяжении-сжатии
При р-сж происходит изм-ие линейных размеров тела: 
- абсолютная продольная деф-ция (абс-ная удлинение)
- относительная прод деф-ция (отн-ое удлинение); 
- абс попер деф-ция
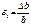- отн-ная попер деф-ция
Между отн-ной прод и отн-ной попер деф-цией сущ-ет зависимость, кот устан-ся опытным путём.
( 
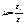) – коэффициент Пуассона – сп-ть мат-ла сопротивляться поперечной деф-ции
0дерево ≤ μ ≤ 0, 5резина; μ = 0, 25 – для стали
Связь между напряжением и деформицией
Впервые эту зависимость установил английский учёный Гук
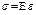
E – модуль продольной упругости (модуль Юнга) – постоянная вел-на для мат-ла хар-ет сп-ть мат-ла сопротивляться прод деф-ции (для стали E = 210 ГПа, дерева E = 10 ГПа)
«Линейная деформация прямо пропорциональна напряжению»
З-н Гука можно записать в виде деф-ции:
- абс-ное удлинение стержня постоянного поперечного сечения.
Для ступенчатого стержня
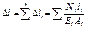
ЕА – жёсткость стержня при р-сж
Определив напряжение можно судить о прочности стержня.
7)8) 
9)Условие прочности
В инженерной практике исп-тся 3-и метода расчёта на прочность.
Рассмотрим 2-а:
1. Расчёт по допускаемому напряжению.
Суть: наиб-ее напряж возн-щее в мат-ле не должно превышать доп-мого напряжения для данного мат-ла:
; 
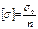( σ 0 – опасное напряжение для пластического мат-ла (стали) равно пределу текучести σ 0 = σ у; для хрупких (чугун, древесина) равно напряжению σ 0 = σ и (определяется опытным путём)).
п – коэф-т запаса прочности, учит-щий общее для всех конструкций факторы:
1). неоднородность мат-ла
2). неточность расчёта нагрузки
Прим-ся в машиностроении
2. Расчёт по предельным состояниям. Исп-ся в строительстве и явл-ся более точным. Здесь использ-ся ряд коэф-тов, каждый из кот учитывает тот или иной фактор.
|
|
|
Суть: не допускать предельного состояния, при кот констр перестаёт удавл-ть экспл-ным требованиям.
R – расчетное сопротивление м-лов опр-тся опытным путём.
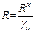
RH – нормативное сопрот-ие устан-ся проектировочными нормами; γ м – коэф-т безопастности по м-лам (учит неодор м-лов). При расчёте констр вводятся и другие коэф-ты: γ с – к-т условий работы, γ н – к-т надёжности.
Условие жёсткости
Наиб относ-ая деф возникает в эл-те констр не должна превышать доп-ого относ-ой деф.
10) Резкое изменение площади поперечн сечен по длине ( отверстия, канавки или надрезы) приводит к неравномерному распредел напряжений, т. е. вызывают концентрацию напряжений и назыв концентраторами.
При исследован явлен концентрац напряжен вводят понятие номинальности напряжений, а так же наибольш тестного напряж и концентрац напряжен.
Наибольш местное напряж- это максимальн напряж действ в месте концентрац напряжений.
Коэффициент концентрации напряжений- это отношение максимальн напряжение к номинальному.
α = γ max/σ ном
α зависит от вида концентрации размеров и формы образца и от свойств материала.
11) Механические характеристики материалов
Мех хар-ки м-ла необх для расчётов эл-тов констр на прочность и жёсткость. Основным опытом для получения мех хар-к для пластич-их м-лов явл-ся испытание на растяжение. Изгот-ся станд-ые образцы, у кот отношение расчётной длины lo к диаметру поперечного сечения do = 10. Машина автом-ки записывает диаграмму зависимости между растяг-щей силой F и удлинением образца ∆ l.
Диаграммы перестраивают в др виде, по оси ординат – нормальное напрчжение σ = N/Aо (Aо – первонач-ая площадь попер сеч образца), по оси абсцисс – относ-ое удлинение ε = ∆ l/lo. Эту диагр наз диагр-мой условных напряжений, т. к. Aо – постоянной применяется в процессе удлинения.
|
|
|
1 – σ pr – предел прямо пропор-ти
1’ – σ e – пр упругости
2 – σ y – пр текучести
3 – σ u - пр прочности
По диаграмме опред-ся мех хар-ка прочности образца: На уч-ке 0-1 деф-ции растут проп-но нагрузке, т. е. вып-ся закон Гука. 1 – предел проп-ти – наиб-ее напряж, для кот спроведлив з-н Гука. Уч-к 0-1’ – м-л испыт-ет только упругие деф-ции (ε е). 1’ – предел упругости – наиб напряж, после кот возние-ет остат-ые деф-ции (ε r). Если нагрузку увелич-ть дальше, то наступит такой момент, когда напряж не увелич-ся, а деф-ция всё равно растёт (1’ – 2). Гориз уч-к – наз площадкой текучести, а состояние м-ла – текучестью. Самая низкая точка на площадке текучести соотв-ет пределу текучести. На этом уч-ке диагр на отполированной пов-ти образца появл-ся очень маленькие трещины (линии сдвигов – линии Людерса-Чернова), они наклонены к оси образца на 40 -500. Претерпев состояние тек-ти м-л снова приобретает сп-ть сопротивляться нагрузке, как бы упрочняться, и диаграмма опять идёт вверх. Предел прочности (σ u) – наиб напряж, кот может выдержать м-л без признаков разрушения. В 3 на образце появл-ся – т. н. шейка – местное сужение попер сечения образца. Площадь сеч в шейке быстро уменьшается, напряж падает и в точке 4 происходит разрыв образца.
12) 
13) Необходимые размеры сечений элементов конструкции определ из расчетов на прочность, жесткость и устойчивость. Расчеты на прочность свод к требованию, чтобы наибольшее напряж в элементе конструкции не превосходят некоторой допустим величины. Существует 3и метода расчета на прочность.
1ый- допустимых напряжений
2ой-предельных состояний
3ий-разрушающих нагрузок
Метод допустимых напряжений требует выполнение 2ух условий σ p ≤ [σ p] σ с ≤ [σ с] или σ ≤ [σ ], где σ - наибольшее по абсолют величине сжимающее или растягивающее расчетное напряжение для материала, [σ ]= σ т/ [nт]; σ p иσ с– наибольшие расчетые напряжения, [σ p] и [σ с]- допустимыенапряжения.
Нагрузка, при которой наибольшее напряжение в конструкции равны допускаемым напряжениям, называется допускаемой.
Метод предельных состояний. В данном случае допустим нагрузку назыв предельно допускаемой нагрузкой, а ее величину определяют путем деления предельной нагрузки на нормативный коэффициент запаса несущей способности. Следует стремиться к тому, чтобы допускаемые напряжения были полностью использованы, т. е. удовлетворять условию σ = [σ ]
|
|
|
Метод разрушающих нагрузок заключаетсяв том чтобы определит максимальные сжимающие и растягивающие напряжения.
14) Необходимые размеры сечений элементов конструкции определ из расчетов на прочность, жесткость и устойчивость. Расчет на жесткость сводиться к требован чтобы наибольш перемещение не превышает допустимой величины.
15) Статический момент плоской ф-ры
Предполож имеем сечение площадью А. выделяем элем-т участок dA. Статич момент относ любой оси х или у назыв сумма произвед элем-ых площадок на рассм до соотв оси.
; 
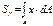
Покажем центр тяжести сечения и его к-т. Точка пересечения осей Х и У и есть центр тяжести сечения.
Координаты центра тяжести находятся из формул ус= 
/А и xс= 
/А
Если известно полож ц. т. фигуры, то статический момент опред-ся: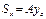 
Статич момент относит оси, кот проходит через ц. т. равны 0. Оси воторые проходят через центр тяжести называбтся центральными осями. Размер-ть Sx, Sy – см3
Статич момент для сложн ф-ры равен сумме статич мом-ов всех сост-щих частей.
; 
Используя запись выраж и определ ц. т. сплошной ф-ры.
; 
16) Осевым моментом инерции сечения относительно некоторой оси называется взятая по всей его площади А сумма произведений элементарных площадок dA на квадраты их расстояний от этой оси, т. е. 
Полярным моментом инерции относительно неторой точки ( полюса) называется взятая по всей его площади А сумма произведений элементарных площадок dA на квадраты их расстояний от этой точки, т. е.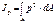 
Центробежный момент инерции сечения относительно некоторых 2ух взаимно перпендекулярных осей называется взятая по всей его площади А сумма произведений элементарных площадок dA на их расстояния от этих осей, т. е.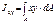 
Моменты инерции имеют размерности см4, м4.
|
|
|
Осевые и полярные момениы всегда положительны, т. к. величины входящие в их вычисления положительны и расстояния в вычислениях беруися в квадрате.
Сумма осевых моментов инерции сечения относительно 2ух взаимно перпенд осей равна полярному моменту инерции этого сечения относительно точки пересечения указанных осей.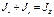 
Центробежн моменты могут быть +, - и =0
Центробежн момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен 0.
|
|
|
