 |
Момент инерции относительно любой оси, кот ║ центральной.
|
|
|
|
17)
Момент инерции относительно любой оси, кот ║ центральной.
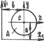Найдём момент инерции относ осей х1, у1, кот ║ х, у и отстают от заданных осей на расст a, b.
; 
Момент инерции относ любой оси равен инерции относ центральной оси плюс произведение площади на квадрат расст между осями.
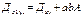
Момент инерции относительно осей, повёрнутых на угол α.
Если известен мом инерции относит двух взаимно ┴ осей ху, то мом инерции относ осей х1 у1, повёрнутых на угол α по отнош к исходным, вычисл по ф-лам.
Доказываемо, что сумма мом инерции при повороте осей не мен, т. е. const.
Ix + Iу = Ix1 + Iу1
При повороте осей один из мом инерции увеличив, другой уменьшается. М. найти такое полож осей, при кот мом ин приним экстремальное знач (одно наиб, др наим-шее). Центробежный мом ин относит этих осей равен 0. Такие оси наз главными.
Положение гл центр осей опред-ся по ф-ле:
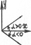Если уг α о > 0, то он откладыв от оси х против хода часовой стрелки (вверх). Если α о < 0, то отклад по ходу часовой стрелки (вниз).
u → ( Ix > Iy ); v → (Ix < Iy )
v ( Ix > Iy ); u (Ix < Iy )
18) Экстремальные значения осевых моментов инерции сечения называются главными моментами инерции. Оси относительно, которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси можно провести через любую т-ку сечения, но в сопротивлении м-лов наиб-ший интерес представляет главные оси, проходящие через ц. т. сечения. Такие оси наз главными центральными осями. Мом инерции относ главных центр осей наз главными центр-ми мом-ми инерции.
Т. обр. гл-ми центр-ми осями наз оси, обладающие след-ми св-вами:
1) проходят через ц. т. сечения.
|
|
|
2) центробежный мом инерции относит этих осей равен 0.
3) мом-ты инерции относит этих осей принимают экстремальное значение.
Главные центральные оси обозначают u, ν .
Главные центраб мом инерции – Iu (max), Iν (min).
Главные центр мом-ты инерции выч по ф-ле
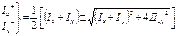
Положение гл центр осей опред-ся по ф-ле:
Если уг α о > 0, то он откладыв от оси х против хода часовой стрелки (вверх). Если α о < 0, то отклад по ходу часовой стрелки (вниз).
u → ( Ix > Iy ); v → (Ix < Iy )
v ( Ix > Iy ); u (Ix < Iy )
Для симметричных ф-р можно сразу провести гл центр оси, одна гл совпад с осью симметрии, а вторая ей ┴ и проходит через центр тяжести сечения.
Радиусом инерции сечения относительно некоторой оси назыв величина определ из равенства
, где i-радиус инерции
19)
|
Построим на главных центральных осях инерции фигуры эллипс с полуосями, равными главным радиусам инерции, причем вдоль оси 
откладываем отрезки 
, а вдоль оси 
— отрезки 
Такой эллипс, называемый эллипсом инерции, обладает следующим свойством. Радиус инерции относительно любой центральной оси 
определяется какперпендикуляр 
проведенный из центра эллипса на касательную, параллельную данной оси. Для получения же точки касания достаточно провести параллельно данной оси любую хорду. Точка пересечения эллипса с прямой, соединяющей центр О и середину хорды, и есть точка касания. Измерив затем отрезок 
, находим момент инерции
|
Круг инерции представляет собой геометрическое место точек, координаты которых в осях построения определяют осевые и центробежные моменты инерции площади относительно любой пары взаимно перпендикулярных осей, проводимых через данную точку. 
Чтобы построить круг инерции, надо располагать значениями трех исходных величин - моментов инерции относительно пары прямоугольных координатных осей, проходящих через заданную точку.
С помощью круга инерции можно графически определить моменты инерции относительно произвольных осей. При этом обычно строят круг инерции по известным моментам инерции Jx, Jy, Jxy, вычисленным относительно произвольных осей Ох и Оу
|
|
|
|
|
|
