 |
Напряжение при кручении. Условие прочности при кручении. Условие жёсткости при кручении. Угол закручивания при кручении
|
|
|
|
Напряжение при кручении
Номальное напряж в попер сечении при круч = 0.
Касат напряж опр по ф-ле:
Мк – крут мом, где располож исслед точка
ρ – расст от цт до точки
IP – полярный момент инерции
Д-мма 1-го сечения 
Из ф-лы видно:
ρ = 0, τ = 0
ρ = ρ тах, τ = τ тах
Условие прочности при кручении
ρ = ρ тах = r
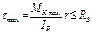
Обозначим
- полярный мом сопрот
; 
RS – расчётное сопрот на срез или сдвиг
WP – полярный мом сопрот наз отнош полярн мом инерции к расстоянию от ц. т. сечения до наиб удалён точки.
46)
Условие жёсткости при кручении
Угол закручивания на уч-ке вала не должен превышать допуск знач [φ ] = 0, 3-30
Угол закручивания при кручении
Угол приходящийся у на единице длины, наз относит углом закруч:
Где 
угол поворота при Z=0. В случае если Mz=const=M, жесткость сечения GJр=const =0
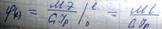
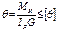
- задается технич условиемиз двух диаметров вала при расчете на прочность и жесткость выбирается больший
Осевой мом сопр для некот сеч:
1. для прокатных профилей (бер из ГОСТа)
2. прямоуг сеч:
3. для круглова:
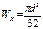
47)
48) 1ая теория прочности основывается на гипотезе о том, что причиной разрушения материала явл наибольшее нормальное напряжение поэтому она называется теоремой наибольших нормальных напряжений.
σ экв= σ 1=σ 0
где σ экв-это эквивал напряж
σ 0 опасное напряж которое = либо σ тек, либо σ врем
В случае сжатия σ экв= 
49) 2ая теория прочности- это критерий наибольших относительных удленений в соответствии с ней при наступлен предельного состояния наибольш удлинения достиг предельн значения = относительному удлинению при одноосновн растяжении
|
|
|
Условное наступление предельного сост записыв следующим образом
Где 
- наибольш относит удлинение соответ рассматрив напряж сост,
- предельн значен относительн удлинения опред из опытов при одноосновн растяжении
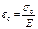
В случае плоского напряж сот где 
Если выразить главное напряжения через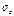 
, 
и τ zy
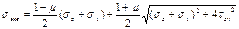
50)
3яя теория прочности исходит из того, что причиной разрушения материала явл. Наибольшие касательные напряжения поэжтому она назыв теорие наибольших касательных напряжений
И условие прочности будет следующим:
где 
- это расчетная величина наибольш касательн напряжен;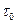 
- Это предельн значен касат напряжен
В случае объемного напряж сост 
наибольш касат напряж определ различно max и min напряж 
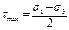
Для плоского напряж сост после подстановки 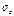, и τ zy
Основной недостаток 3ей теории прочности состоит в том, чтов случ объхемн напряж сост в данной теории не учитыв влияние σ 2
51) Энергетическая теория прочности исходит из предложения о том, что количество удельной потенциальной энергии деформации накопленой к моменту наступлен опасного сост мат одинаково как при любом сложном напряж сост так и при простом растяжен. В соответствии с этим в основу данной теории первоначально была полож гипотеза связывающая причина наступления опасного сост материала с полной удельн потенциальной энергией достигающ своего предельного значения U< U0, где U=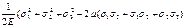 
Полная удельная энергия
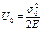предельное значение энергии определ из опыта на прост растяжение.
Данная гипотеза неоправдана на опыте, т. к. эксперемент доказано, что при всесторонем давлении пластич деформац не появляется даже при сверхвысоких давлениях хотя при этом большая удельная потенциальная энергия. Позже было высказано предложение, что в качестве критерия прочности материала приним не вся удельная энергия, а лишь та ее часть которая накаплитв в следствии изменения формы кубика с ребром = 1
|
|
|
52)
В теории прочности Сора устанавл опр зависим прочностн свойств материала от вида его напряж сост. Для получения и обоснования такой зависимости исп предлож Мором круги напряжений
получить действ огибающ предельных кругов сложного поэтому на практике огибающ заменяют прямыми, касательными лишь к 2ум кругам, которые строят по данным опытана растяж и сжатие( прямые- границы облости прочности.
теория прочности (т. Морра) учитывает, что прочность мат-ла опред σ 1 и σ 3:
|
|
|
