 |
20) Момент инерции простых ф-р относ их центральных осей.
|
|
|
|
20) Момент инерции простых ф-р относ их центральных осей.
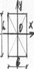 1)
1)  ;
;  ;
; 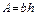
 2)
2) 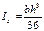 ;
;  ;
; 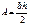
3) 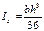 ;
;  ;
; 
 4)
4)  ;
; 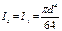
5) С = 0, 212d; Ix = 0, 00686d4; 
21) Изгиб - это такой вид деформации бруса, при котором в его поперечн сечениях возникают изгибающ моменты. Если в поперечных сечениях возникают и поперечные силы, то изгиб называется поперечным. Если поперечные силы отсутствуют, то такой изгиб называется чистым. С геометрической точки зрения изгиб характерез тем, что ось бруса прямолинейна до деформации становится кривой линией ( изгибается ось бруса).
Деформ изгиба возникает при нагружении бруса силами действ в плоскости проходящ через его продольную ось и перпенд этой оси и парами сил действующ в этих же плоскостях.
В случаи если все нагрузки и реакции связи действ в одной плоскости изгиб называется плоским.
Допущения: 1) продольные волокна бруса параллельные его оси испытывают лишь деформац растяжения или сжатия и не вызывают давления друг га друга; 2) кажд поперечн сечен мтержня плоское до деформации остается плоским и нормалью к оси после деформац.
Для того чтобы балка могла воспринимать нагрузку и передавать ее на основание онадолжна быть соединена с ними опорными связями:
-шарнирно-подвижная
-шарнирно-неподвижная
-заделка
Определение опорных реакции осуществляется с помощью равенств ∑ Y = 0 ∑ Х = 0 ∑ Ма = 0
22)
 При изгибе в попер сеч балки возник внутр силы – силы упругости, кот так же опред методом сечений.
При изгибе в попер сеч балки возник внутр силы – силы упругости, кот так же опред методом сечений.
Рассм равновесие правой части: для её равновесия в попер сеч необх прилож попер силу Q и изгиб мом Mизг, кот замен действие отброш части. Попер сила Q в люб сеч числ = алгебр сумме проекций всех сил на пл-ть сеч, кот действ по одну стор от сеч.
|
|
|
правило знаков при плоском изгибе:
«если внешняя сила или мом стремится изогнуть балку относит сеч вверх, то Mизг > 0, если вниз, то Mизг < 0».
 Для оценки прочн балки необх строить эпюры внутр сил.
Для оценки прочн балки необх строить эпюры внутр сил.
Эпюры изгиб мом строятся на растянутых волокнах балки.
Деф завис-ти при изгибе
Между М, Q, q сущ след зависимость
 - теорема Журавского
- теорема Журавского

 - 1-ая произв от попер силы по длине = интенсивности распред нагрузки.
- 1-ая произв от попер силы по длине = интенсивности распред нагрузки.
 - 1-ая произв от изгиб мом по длине = попер силы.
- 1-ая произв от изгиб мом по длине = попер силы.
23) Правило для контроля правильности построения эпюр:
1. на уч-ке, где q = 0 попер сила постоянна (Q = const).
 ,
,
а изгиб мом измен по линз -ну

2. на уч-ке, где q = const, попер сила изм по линз –ну
 ,
,
А изгиб мом по порабол з-ну


 3. в местах прилож силы на эпюре Q имеется скачёк на вел-ну этой силы, на эпюре мом излом.
3. в местах прилож силы на эпюре Q имеется скачёк на вел-ну этой силы, на эпюре мом излом.
4. в местах прилож мом, на эпюре мом им-тся скачёк = вел-не мом. На эпюре силы никак не измен.
5. в местах перех попер силы через 0 изгиб мом приним экстрем знач.
24) Чистый изгиб:
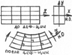 - когда в попер сеч будут возник только изгиб моменты.
- когда в попер сеч будут возник только изгиб моменты.
Из этого след, что:
1. прод волокна испыт плоское раст-сж. Сущ слой балки, кот не деф, наз нейтральным слоем, в попер сеч нейтральная ось.
2. гипотеза плоских сеч подтв – плоск сеч после деф ост плоскими.
 3. в сеч отсутствует τ (касат напр-е), нет сдвига, т. к. углы сетки остались прямыми.
3. в сеч отсутствует τ (касат напр-е), нет сдвига, т. к. углы сетки остались прямыми.
На основе этих предполож и гипотез выводится ф-ла для опред норм напряж в люб точке сеч:

Мх – изгиб мом в сеч, где располож исслед точка.
Iх – осевой мом инерции сеч, относит нейтр оси.
у – расст от н. о. до точки, в кот опред напряж.
Норм напряж при изгибе
При плоском попер изгибе в кажд точке попер сеч балки возник норм и касат напряж.
Устан связь между напряж и внутр усилиями.

 Попер силой Q наз равнод всех внутр касат сил в попер сеч
Попер силой Q наз равнод всех внутр касат сил в попер сеч


Изгиб мом Мх наз результир мом всех внутр норм сил действ в попер сеч.
|
|
|
Эпюра распред норм напряж в попер сеч.
Устан, что нейтр линия проходит через ц. т. сеч. Ось симметрии так же явл нейтр линией.
1) симметричное сеч:


Из ф-лы видно: если у = 0 => σ = 0, у = утах => σ = σ тах

2) несимметричн сеч относ н. о.:
Вывод: на нейтр линии норм напряж в сеч = 0, а в точках наиб удал от нейтр оси σ тах.
Ф-лу можно предст в др виде
 - осевой мом сопротивления
- осевой мом сопротивления
тогда ф-ла для опред напряж:
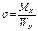 - для симм-ных сеч, заключ в прямоуг(, двутавр, ][ ).
- для симм-ных сеч, заключ в прямоуг(, двутавр, ][ ).
Осевой мом сопр (Wx) наз отнош осевого мом инерции к расст от н. о. до наиб удал точки.
|
|
|


