Задача 54. Допускаемое продольное усилие в пружине (см. решение задачи 53)

Задача 54

Гружёная тележка массой 42000 кг останавливается, ударяясь в два неподвижных буфера, показанных на рисунке. Допускаемое касательное напряжение в витках пружин [t] =500МПа. Пружина имеет 12 рабочих витков и предварительно подтянута на 10мм. Наименьший зазор между витками 3мм. Индекс пружины с = D/d = 100: 25 =4, поправочный коэффициент k=1. 38. Модуль упругости материала проволоки G =8*10⁴МПа.

Определить допускаемую скорость тележки в момент удара и вычислить высоту пружины в свободном состоянии.

 

Порядок решения:

Допускаемое продольное усилие в пружине (см. решение задачи 53)

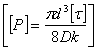= =22220Н.

Осадка пружины .

Жёсткость пружины С =P/l = 22220/68 =326, 8 Н/мм.

Согласно условию задачи предварительная деформация пружины l₀ =10мм.

При изменении деформации от l₀ до l каждая из двух пружин поглощает половину кинетической энергии тележки, т. е. работа сжатия пружин уменьшает кинетическую энергию тележки до нуля. Обозначив массу тележки- m и скорость её движения - ν, пренебрегая потерями на трение, получим равенство 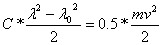, откуда

= =265мм/с =15, 9м/мин.

При заданном наименьшем зазоре между витками 3мм необходимая в свободном состоянии высота пружины H = z(d+3) +d +l = 12*(23+3) +25 +68 =430мм.

 

Задача 55

Спроектировать цилиндрическую пружину кручения из проволоки круглого сечения. Максимальный момент М_к = 5000Нмм, необходимый угол закручивания a=180⁰, допускаемое напряжение изгиба материала проволоки [s_и] =500МПа, индекс пружины c =D/d =8, (где d – диаметр проволоки, D – средний диаметр пружины). Модуль упругости материала пружины Е = 2*10⁵МПа. Коэффициент, учитывающий кривизну прутка вычислить по формуле .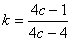

Порядок решения:

При нагружении пружины в каждом её сечении действует момент М, равный внешнему закручивающему моменту. Этот момент направлен вдоль оси пружины и раскладывается на момент М_и= М*Сosa - изгибающий виток и крутящий момент М_к= М*Sina (a- угол подъёма витка). При расчёте пружины на кручение нас интересует напряжение изгиба, которое получается от закручивания и вычисляется по формул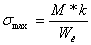е , где 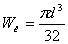- момент сопротивления изгибу сечения проволоки, - коэффициент учитывающий кривизну прутка. Подставляя значения, получим требуемый диаметр проволоки

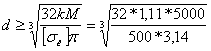= 4, 8мм. Принимаем проволоку диаметром 5мм.

Средний диаметр пружины D =c*d =8*5 =40мм.

Угол закручивания пружины (рад) может быть определён как угол взаимного упругого наклона концевых сечений бруса длиной L, ( равной суммарной длине витков пружины), под действием чистого изгиба

, где L =p*D*z - длина пружины, J= - момент инерции сечения проволоки, z – рабочее число витков пружины. Преобразовывая угол закручивания в градусы, определяем необходимое количество витков пружины

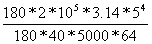= =31, 2

Шаг витков пружины t = d + 0. 5мм = 5, 5мм.

Высота пружины из принимаемого зазора между витками 0, 5мм,

Н = z*(d+0. 5) =31*5. 5 = 170, 5 мм.

Задача 56

Определить степень подвижности, представленного на рисунке пятизвенного механизма. Все звенья соединены шарнирно. Звено АС = ДF. Звено СД = АF. Улучшить схему механизма.

 

Порядок решения:

Имеем плоский 5-тизвенный шарнирный механизм, степень подвижности которого определяется по формуле: W = 3n - 2P5 - P4, где n =4 - число подвижных звеньев, Р5 = 6 - число кинематических пар пятого класса, Р4 = 0 - число кинематических пар четвёртого класса.

W = 3*4 - 2*6 - 0 = 0.

Вывод - представленный механизм имеет нулевую степень подвижности, т. е. работать не может. Механизм сможет работать, если звено ВЕ выполнить параллельно звену СД.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: