 |
Примеры решения задач. Решение. Рассмотрим частицу в одномерной потенциальной яме с бесконечно высокими стенками (см. Найдем волновую функцию частицы. Для нее мы ожидаем:
|
|
|
|
Примеры решения задач
Задача 1. Показать, что ограничение частицы в пространстве вызывает квантование ее энергии.
Решение
Рассмотрим частицу в одномерной потенциальной яме с бесконечно высокими стенками (см. рис. 5. 5).

|
| Рис. 5. 5 |
Найдем волновую функцию частицы. Для нее мы ожидаем:
·Y(х) = 0 вне ямы;
· Y(0) = Y(L) = 0 на стенках ямы;
· Y(х) должна быть волной или суммой волн, т. к. представляет частицу и должна быть связана с деБройлевской волной.
Пусть волновая функция имеет вид:

Она должна вписываться в «ящик» (рис. 5. 6):

|
| Рис. 5. 6. |
Это означает, что целое число полуволн должно укладываться на длине L
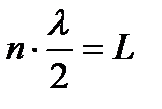
или возможные длины волн равны:
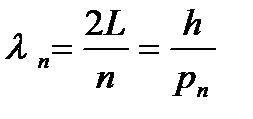 ,
,
где n = 1, 2, 3, …..
Отсюда получаем возможные значения импульсов частицы в яме:

Полная энергия частицы в пределах ямы равна кинетической энергии, т. к. потенциальная энергия в яме U = 0 и частица является свободной:
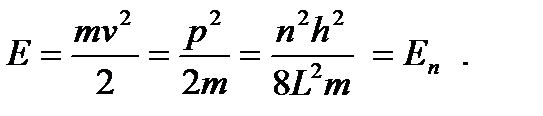
Итак, частица обладает не любой энергией, а вполне конкретной, зависящей от целого числа n
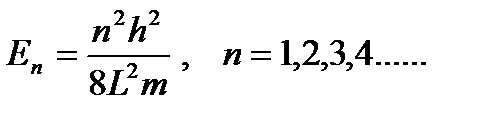 ,
,
где n – главное квантовое число.
Таким образом, действительно ограничение движения частицы в пространстве приводит к квантованию ее энергии. Это же должно быть справедливо и для электрона в атоме водорода.
Отметим, что энергия частицы с Е = 0 отсутствует, т. к. соответствующая ей волна не существует. Таким образом, минимальная энергии частицы в потенциальной яме соответствует состоянию с квантовым числом n=1:
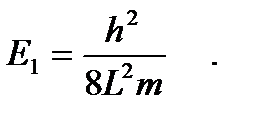
Задача 2. Частица находится в одномерном потенциальном ящике шириной L. Найти среднее положение частицы в основном состоянии.
Решение
По определению средняя координата частицы определяется из соотношения
|
|
|
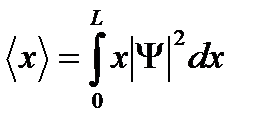
Волновая функция частицы в потенциальной яме (см. предыдущую задачу)
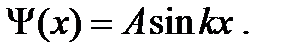
Из требования
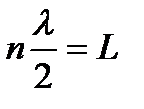
длина волны основного состояния, для которого n = 1, равна 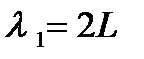 , а волновой вектор
, а волновой вектор
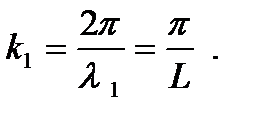
Волновая функция основного состояния имеет вид: 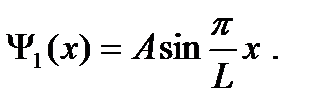
Волновая функция должна быть нормирована: 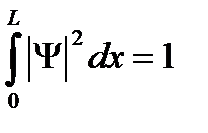 .
.
Из условия нормировки находим амплитуду волновой функции А:
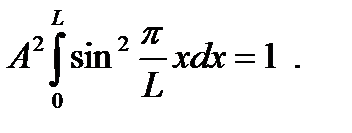
Вычислим интеграл:
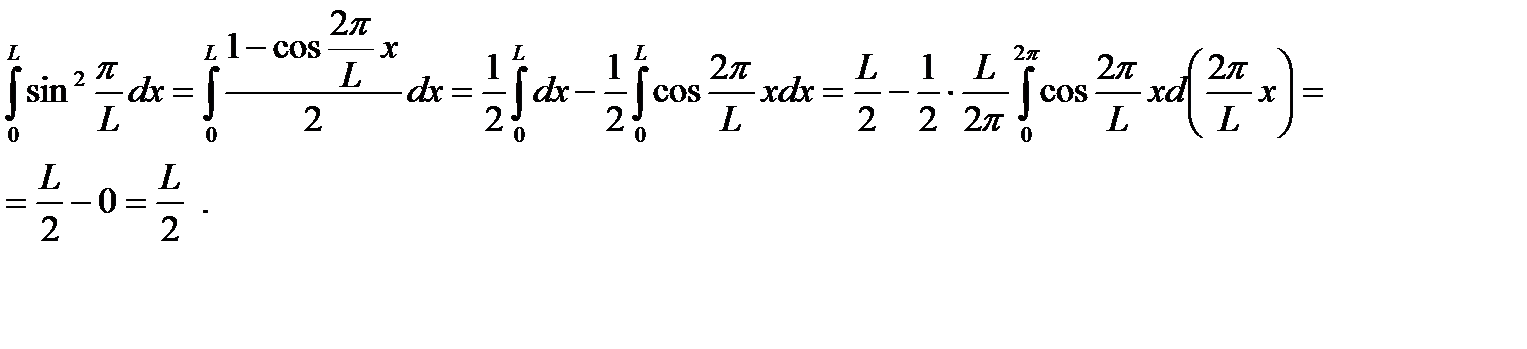
Получаем: 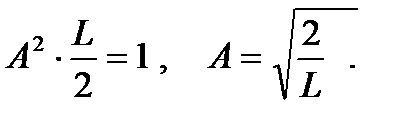
Итак, волновая функция основного состояния имеет вид:
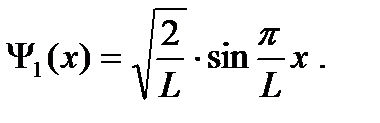
Находим среднюю координату частицы:
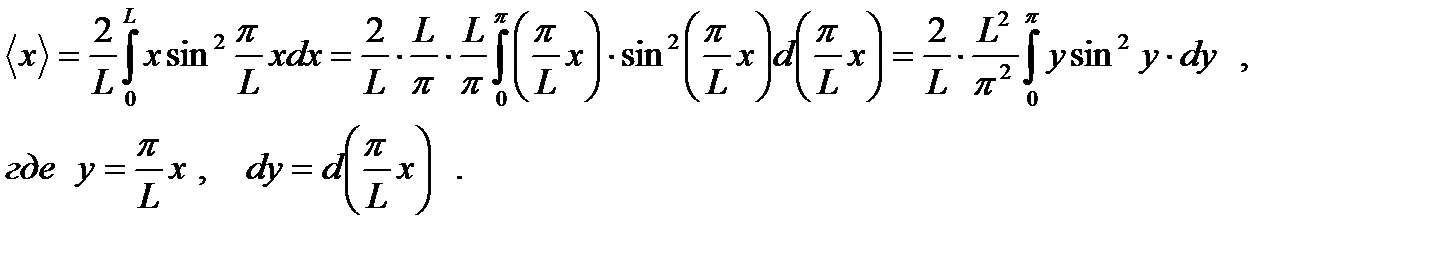
Вычислим интеграл:

В результате получаем: 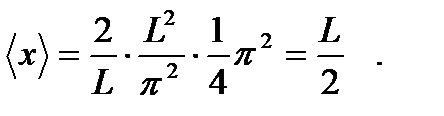
Видно, что частица находится в середине ящика, что и следует из плотности вероятности 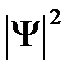 :
:

Рис. 5. 7. Частица в потенциальной «яме»
с бесконечно высокими стенками
Задача 3. Какова ширина (l) одномерной потенциальной ямы с бесконечно высокими стенками, если при переходе электрона со второго квантового уровня (n1 = 2) на первый (n2 = 1) излучается фотон с энергией Е = 1 эВ?
| Дано: n1 = 2 n2 = 1 Е = 1 эВ | СИ: 1. 6× 10-19 Дж |
| l -? |
Решение
Запишем уравнение для энергии электрона на заданных стационарных уровнях:
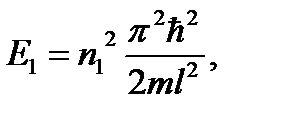
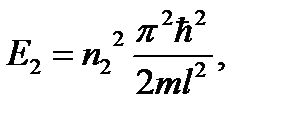
По условию задачи при указанном переходе выделяется квант энергии:
Δ Е = Е1 – Е2.
Подставим значения соответствующих энергий и получим уравнение:
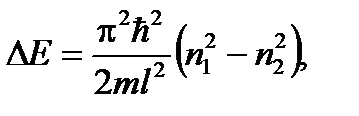
Из последнего уравнения выразим искомую величину – ширину ямы (l):
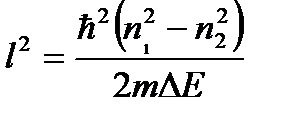
Подставим численные значения и сделаем расчет:
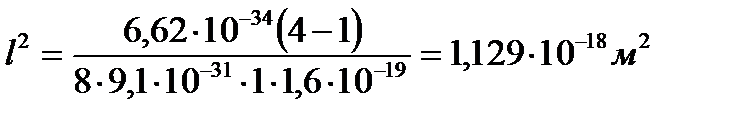
Ответ: l = 1, 062 10-9 м.
Задача 4. При какой ширине (l) потенциальной ямы дискретность энергии микрочастицы, находящейся в ней, сравнима с энергией теплового движения при температуре Т.
Решение
Запишем уравнение для собственных энергий электрона в атоме для стационарных уровней с номерами n и (n + 1):
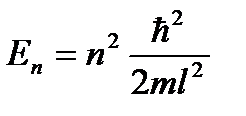 и
и 
Запишем дискретность энергии микрочастицы для указанных состояний с номерами n и (n + 1):
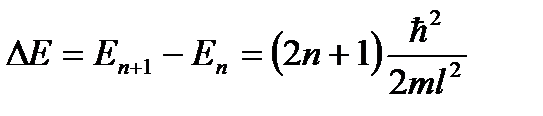
По условию 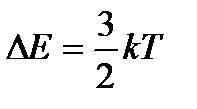 , поэтому можно записать:
, поэтому можно записать:
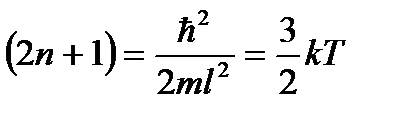
Решаем полученное уравнение относительно ширины ямы – l
|
|
|

Ответ: 
|
|
|


