Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими стенками

Рассмотрим поведение частицы, в потенциальном поле, показанном на рис. 5. 1.

 Для простоты рассмотрим одномерный случай, когда частица движется вдоль оси Ox. Такая «яма» описывается потенциальной энергией:

 

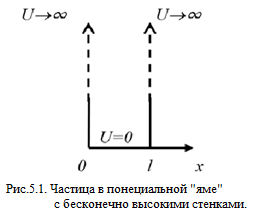
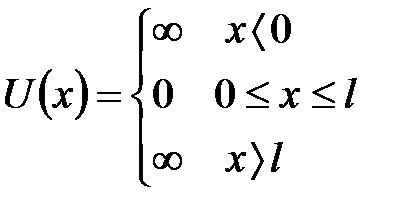
где l – ширина ямы, а энергия отсчитывается от ее дна.

Запишем уравнение Шредингера для стационарных состояний в случае одномерной задачи:

 

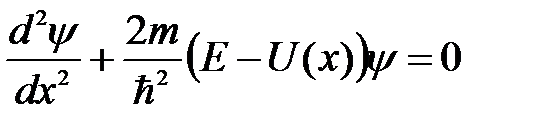                         (5. 16)

По условию задачи (яма имеет бесконечно высокие «стенки») частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения, а, следовательно, и волновая функция, за пределами ямы равны нулю. На границах «ямы» (x= l и x = 0) волновая функция, вследствие непрерывности, также должна обращаться в нуль. Следовательно, граничные условия принимают вид:

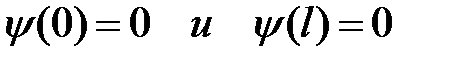.                                               (5. 17)

Тогда в пределах ямы уравнение (5. 16) сведется к уравнению

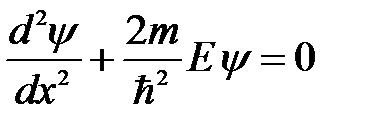,                                                                        (5. 18)

или

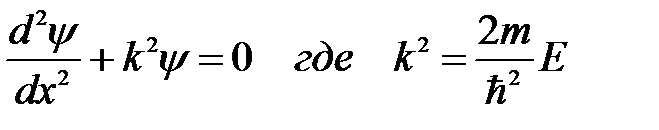.                        (5. 19)

Общее решение уравнения (5. 19) запишем в виде:

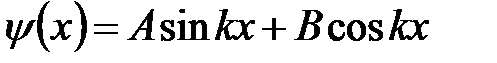.            (5. 20)

Используя первое граничное условие из (5. 17), получим В = 0, тогда решение (5. 20) принимает вид:

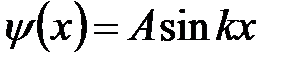.                                                            (5. 21)

Используя второе граничное условие из (5. 17), получаем, что kl = np, где n – целое число, следовательно,

.                                                                                 (5. 22)

Условие (5. 22) имеет простой физический смысл. Так как волновое число связано с длиной волны

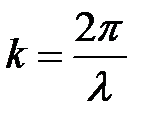,                                             (5. 23)

где l – длина волны де Бройля для микрочастицы, то приравняв правые части (5. 22) и (5. 23), получим:

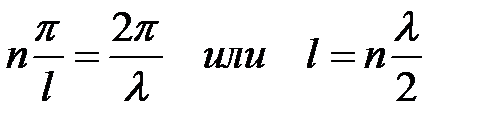.                    (5. 24)

Следовательно, на длине ямы (l) должно укладываться целое число длин полуволн (l/2), т. е., образуется стоячая волна, причем возможные длины волн l_n принимают дискретный ряд значений. Из уравнений (5. 14) и (5. 23) следует, что энергия частицы в потенциальной «яме» равна:

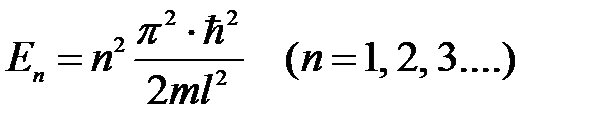.                (5. 25)

Из уравнения (5. 25) следует, что энергия частицы в потенциальной яме не может быть любой. Она принимает лишь ряд дискретных собственных значений Е_n. Другие значения энергии невозможны. Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными. Следовательно, энергия частицы в потенциальной яме квантована.

Квантованные значения энергии называются уровнями энергии, а числа n, которые определяют энергетические уровни частицы, называются квантовыми числами. Таким образом, частица в потенциальной яме может находиться на определенном энергетическом уровне, иногда говорят, в определенном квантовом состоянии n.

Интервал между соседними энергетическими уровнями равен

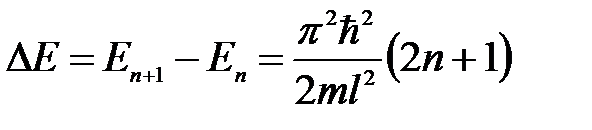.                             (5. 26)

Для «ямы», размеры которой соизмеримы с размерами атома (l = 10^{-9 м),}

,

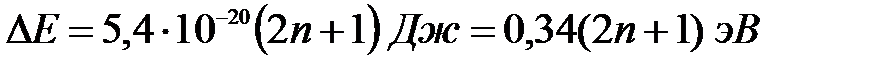Для «ямы» макроскопических размеров (l = 10² м)

.

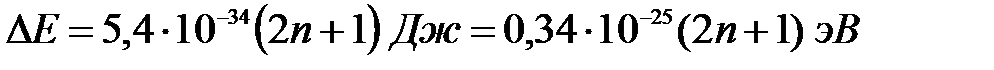В последнем случае энергетические уровни расположены так тесно, что их можно считать квазинепрерывными. Для такой потенциальной «ямы» квантование энергии дает результаты, мало отличающиеся от результатов классической физики. Отметим, что DЕ → 0 при l ® ¥, т. е., энергетический спектр свободной частицы будет непрерывным.

Квантово-механическое решение данной задачи приводит к выводу, что частица в потенциальной «яме» не может иметь энергию, меньшую, чем минимальная энергия, равная

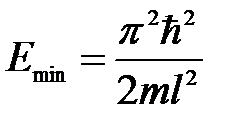.                                           (5. 27)

Рассмотрим влияние квантового числа n на характер расположения энергетических уровней частицы в потенциальном «ящике». Сравним интервал между соседними энергетическими уровнями с энергией частицы, находящейся на n -м уровне, используя соотношения (5. 26) и (5. 27):

.                                                   (5. 28)

Тогда для больших квантовых чисел n > > 1 (т. е. 2n +1≈ 2n ) получим:

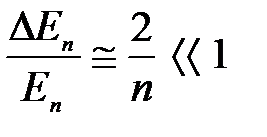,                                                    (5. 29)

т. е., соседние уровни расположены тем теснее, чем больше n. Этот результат является частным случаем принципа соответствия Бора – при больших значениях квантовых чисел законы квантовой механики должны переходить в законы классической физики. Например, согласно гипотезе де Бройля, волновые свойства присущи всем телам, однако в случае макроскопического тела волновыми свойствами можно пренебречь, т. е., применять классическую механику Ньютона.

Запишем собственные y -функции, подставив в уравнение (5. 21) значения k (5. 23):

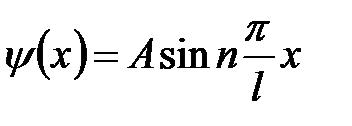.                                              (5. 30)

Постоянную Aнайдем из условия нормировки:

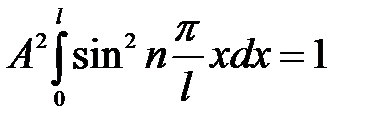.                                            (5. 31)

Решая уравнение (5. 31) относительно A, получим:

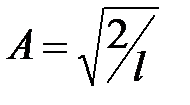.                                                            (5. 32)

Окончательно, собственные y -функции будут иметь вид:

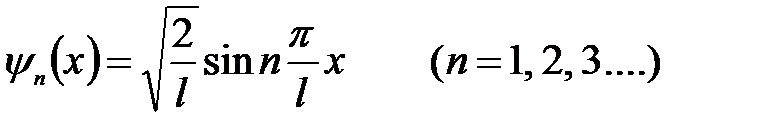.                                   (5. 33)

На рис. 5. 2 представлено поведение собственных функций y_n(x) и плотности вероятности обнаружения частицы |y_n(x)| ² в различных точках “ямы” для трех энергетических уровней при n = 1, 2, 3:

 

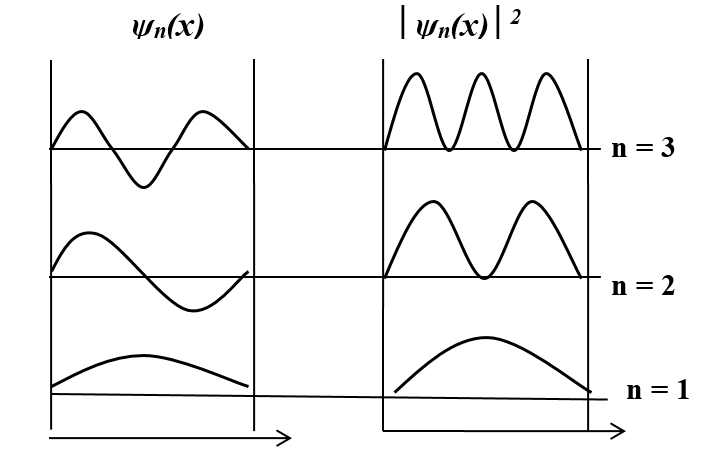
Рис. 5. 2. Собственные функции y_n(x) и плотность вероятности обнаружения частицы |y_n(x)| ² в различных точках “ямы”

 

Из рис. 5. 2 следует, что в квантовом состоянии при n = 2 частица не может находиться в середине ямы, но одинаково часто может встретиться в точках с координатами 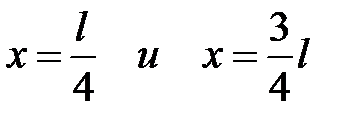, что еще раз свидетельствует, о несостоятельности представлений о траекториях частицы в квантовой механике.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: