 |
Задача 3. Кинетическая энергия электрона в атоме (К) составляет величину 10 эВ. Оценить минимальные размеры атома, используя соотношение неопределенностей.
|
|
|
|
Задача 3. Кинетическая энергия электрона в атоме (К) составляет величину 10 эВ. Оценить минимальные размеры атома, используя соотношение неопределенностей.
| Дано: К = 10 эВ me = 9. 11× 10-31 кг | СИ: 1. 6× 10-18 Дж |
| lmin -? |
Решение
Электрон находится в атоме, линейные размеры которого l. Следовательно, неопределенность координаты равна:
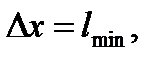
Запишем соотношение неопределенностей, подставив величину Δ х:
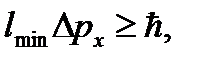
где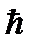 
= 1. 054× 10-34 Дж× с – постоянная Планка.
Поскольку надо найти минимальные размеры атома, то Dpx не должно превышать px, т. е. Dpx= px. Импульс связан с кинетической энергией электрона соотношением:
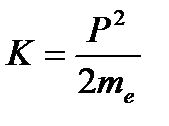
Из последнего уравнения выразим импульс электрона, подставим его в соотношение неопределенностей и решим полученное уравнение относительно минимально линейного размера атома:
Подставив числовые значения, рассчитаем минимальный размер атома:
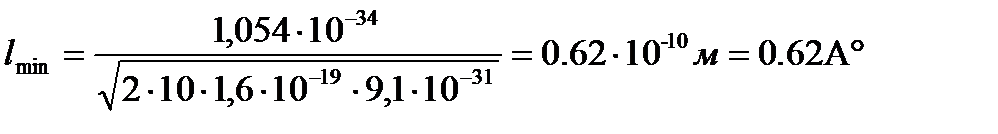
Ответ: lmin = 0. 62 Å.
Задача 4. Атом излучает фотон с длиной волны 550 нм. Время излучения 10-8 с. Определить неточность в определении указанной длины волны и с какой точностью может быть определено местонахождение данного фотона в направлении его движения.
| Дано: l = 550 нм Dt = 10-8 с c = 3× 108 м/c | СИ 5. 5× 10-7 м |
| Dl -? Dx -? |
Решение
Запишем уравнение для расчета энергии кванта (фотона):
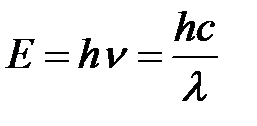
Для нахождения неточности в определении указанной длины волны (Δ λ ) возьмем производную от энергии по длине волны и выразим неточность в определении энергии кванта Δ Е:
Запишем соотношение неопределенностей для энергии и выразим из него неточность в определении энергии излученного кванта (фотона) Δ Е:
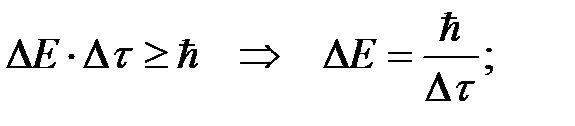
Приравняем выражения для величины Δ Е, полученные выше. Решим последнее уравнение относительно искомой величины Δ λ:
|
|
|
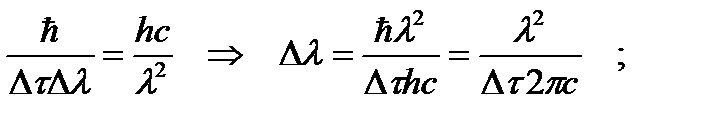
Запишем уравнение де Бройля относительно импульса фотона. Возьмем производную от импульса по λ и выразим неточность в определении его импульса Δ Р:
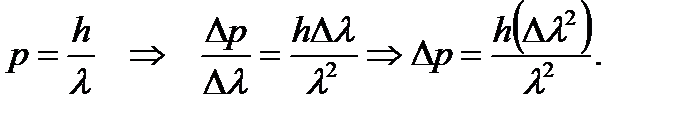
Используем соотношение неопределенностей для расчета величины неточности в определении координаты фотона Δ Х:
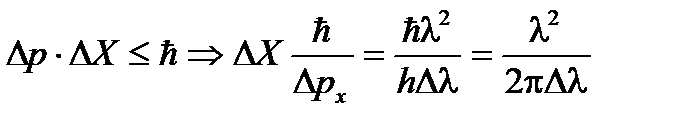
Произведем вычисления заданных величин:
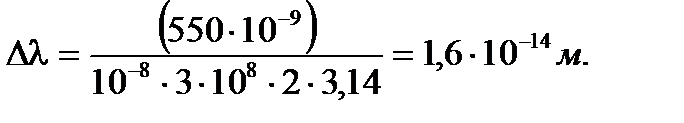
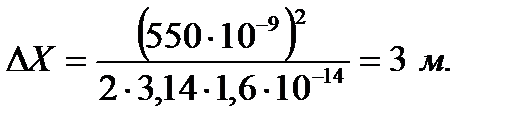
Ответ: 
Тема 5: «Волновая функция. Уравнение Шредингера. Движение заряженных частиц в потенциальной «яме» с бесконечно высокими «стенками». Туннельный эффект».
Краткая теория
Вероятностный смысл волн де Бройля. Волновая функция
Волны де Бройля, связанные с движущимися частицами, имеют специфическую квантовую природу, не имеющую аналогии в классической физике.
Из опытов по дифракции электронов обнаруживается неодинаковое распределение пучков электронов, отраженных или рассеянных по различным направлениям – в некоторых направлениях наблюдается большее количество электронов, т. е. вероятность попадания электронов в различные точки экрана наблюдения неодинакова. С волновой точки зрения это соответствует большей интенсивности волн де Бройля в этих направлениях. Другими словами, интенсивность волн в данной точке пространства определяет число электронов, попавших в эту точку за 1 с. Это послужило основанием для статистического, вероятностного истолкования волн де Бройля.
Квадрат модуля амплитуды волны де Бройля в данной точке пространства является мерой вероятности того, что частица обнаруживается в этой точке
ê Aê 2 ~ W. (5. 1)
Для описания распределения вероятности нахождения частицы в данный момент времени в некоторой области пространства вводится волновая функция y (x, y, z, t), о пределяемая следующим образом: вероятность (dW) того, что частица находится в элементе объема (dV) пропорциональна квадрату модуля волновой функции |y| 2 и элементу объема (dV):
|
|
|
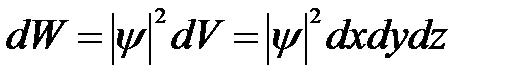(5. 2)
где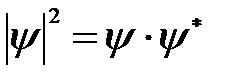 
, y * - функция, комплексно сопряженная с y.
Величина |y| 2 имеет смысл плотности вероятности:
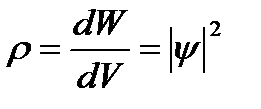, (5. 3)
то есть, определяет вероятность нахождения частицы в данной точке пространства. Иными словами |y| 2 определяет интенсивность волн де Бройля. Таким образом, физический смысл имеет не сама y - функция, а квадрат ее модуля |y| 2.
Вероятность обнаружения микрочастицы в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна:
(5. 4)
Волновая функция должна удовлетворять условию нормировки:
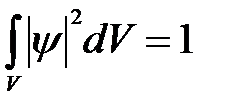. (5. 5)
Уравнение (5. 5) означает, что нормировать y - функцию следует таким образом, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это условие говорит об объективном существовании частицы во времени и пространстве. Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду требований, а именно:
y - функция должна быть:
1) конечной, так как вероятность не может быть больше единицы;
2) однозначной, так как вероятность не может быть многозначной величиной;
3) непрерывной, так как вероятность не может изменяться скачками.
Волновая функция удовлетворяет суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями y1, y2, y3, ….. yn, то она может находиться в состоянии y, описываемом линейной комбинацией этих функций
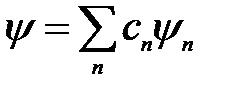. (5. 6)
Знание волновой y - функции позволяет в квантовой механике вычислять средние значения физических величин.
|
|
|
