 |
Уравнение Шредингера. Движение свободной частицы
|
|
|
|
Уравнение Шредингера
В классической физике второй закон Ньютона позволяет решать основную задачу – по заданным силам, действующим на тело, и по начальным условиям определить в любой момент времени координаты тела, его скорость, т. е., описать движение тела в пространстве и во времени. В квантовой механике необходимо учесть двойственную природу микрочастиц, которая ограничивает возможность применения к таким частицам классических понятий о координате и скорости. Это уравнение должно быть таким, чтобы позволяло учесть волновые свойства частиц. Поскольку положение частицы в пространстве задается в квантовой механике через волновую функцию y (x, y. z. t), то основное уравнение квантовой механики должно быть уравнением относительно функции y (x, y. z. t). Это уравнение должно быть волновым, ибо из него должны получить свое объяснение опыты по дифракции микрочастиц.
Основное уравнение квантовой механики было найдено в 1926 году Э. Шредингером. Как и законы Ньютоны, уравнение Шредингера не выводится, а постулируется. Справедливость данного уравнения подтверждается тем, что выводы квантовой механики, полученные с его помощью в атомной и ядерной физике, находятся в хорошем согласии с опытом. Уравнение Шредингера имеет вид:
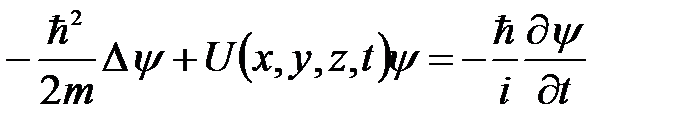, (5. 7)
где m – масса частицы; U(x, y, z, t) – потенциальная энергия частицы в силовом поле, где она движется;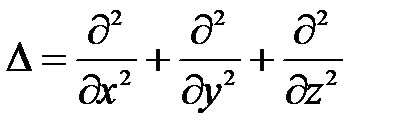 
- оператор Лапласа, y = y (x, y, z, t) - искомая волновая функция.
Уравнение (5. 7) называют временным или общим уравнением Шредингера. Оно справедливо для любой частицы с массой m, которая движется со скоростью V< < c. Решение уравнения (5. 7) можно представить в виде:
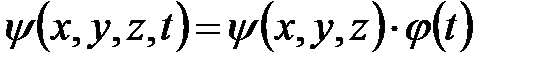, (5. 8)
|
|
|
где y (x, y, z) - координатная или амплитудная часть волновой функции; j(t) - временная часть волновой функции.
При решении ряда физических задач микромира необходимо уметь находить стационарные, т. е., не содержащие времени, решения уравнения Шредингера. Это имеет смысл в тех случаях, когда потенциальная энергия частицы не зависит от времени U = U(x, y, z). Решением в этом случае будет волновая функция вида y =y(x, y, z), т. е. ее амплитудная часть. Уравнение Шредингера, соответствующее этому решению, принимает вид
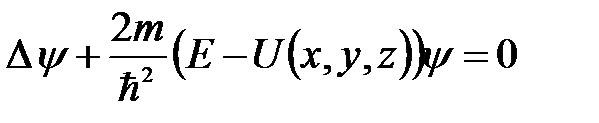, (5. 9)
где m – масса частицы; Е –полная энергия частицы; D - оператор Лапласа.
Это уравнение называется стационарным уравнением Шредингера.
Волновые функции y =y(x, y, z, t), удовлетворяющие уравнению Шредингера при данном U = U(x, y, z), называют собственными функциями. Значения полной энергии (Е), при которых существуют решения уравнения Шредингера (5. 9), называются собственными значениями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае будет присутствовать сплошной спектр энергий, а во втором – дискретный.
Движение свободной частицы
Свободная частица – это частица, движущаяся в отсутствие внешних полей. Рассмотрим частицу, которая движется вдоль оси Ох, то есть, будем решать одномерную задачу. Поскольку частица свободная, на нее не действуют силы и ее потенциальная энергия U(x) = const. Положим U(x) равной нулю. Тогда полная энергия этой частицы совпадает с кинетической и стационарное уравнение Шредингера (5. 9) принимает вид:
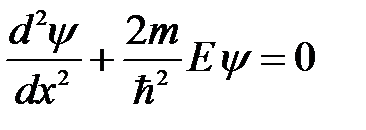; (5. 10)
если ввести обозначение
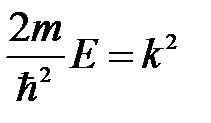, (5. 11)
то уравнение (5. 10) можно записать в виде:
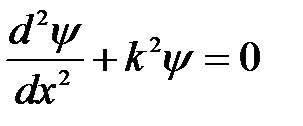. (5. 12)
Решение уравнения (5. 12) имеет вид
y(x) = A× eikx, (5. 13)
|
|
|
где A = const и k = сonst.
Собственные значения энергии получим из (5. 11):
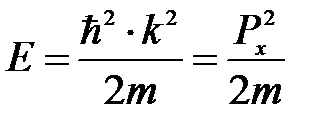. (5. 14)
Зависимость энергии от импульса частицы имеет вид, типичный для нерелятивистской частицы. Следовательно, энергия свободной частицы (Е), как и волновое число (k), может принимать любые значения, т. е., ее энергетический спектр является непрерывным. Таким образом, свободная микрочастица описывается плоской монохроматической волной де Бройля. Этому соответствует плотность вероятности обнаружения частицы в данной точке пространства, которая не зависит от времени:
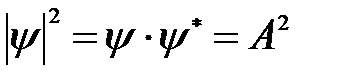, (5. 15)
т. е. все положения частицы в пространстве равновероятны.
|
|
|
