 |
Прохождение частицы сквозь потенциальный барьер.
|
|
|
|
Прохождение частицы сквозь потенциальный барьер.
Туннельный эффект
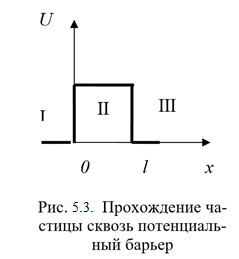
Качественное различие свойств макро- и микрочастиц особенно резко сказывается в их поведении при встрече с потенциальным барьером. Предположим, частица движется вдоль оси Ох в таком силовом поле, когда область движения частицы разделена потенциальным барьером.
U(x) = 0 при x < 0 и x > l,
U(x) = const при 0 < x < l.
Если полная энергия частицы E < U, то с классической точки зрения частица может двигаться лишь в областях I и III (x < 0 или x > l). Проникнуть в область барьера она не может, так как там ее кинетическая энергия, равная Eк= E – U, оказалась бы отрицательной, что невозможно. Такая частица не может перейти из области I в область III. По-иному проявляет себя микрочастица, поведение которой описывается уравнением Шредингера. Волновая функция в этом случае будет отлична от нуля и в области II, благодаря чему вероятность ее проникновения из области I в область III окажется отличной от нуля. Следовательно, микрочастица с энергией, меньшей, чем высота барьера, способна пройти («просочиться») сквозь потенциальный барьер. Это явление называется туннельным эффектом, для его описания вводится коэффициент прозрачности D потенциального барьера. Если, по аналогии с оптикой, для волн де Бройля подсчитать интенсивность падающей на барьер волны (Iпад) и интенсивность волны, прошедшей сквозь барьер (Iпрох), то прозрачностью, или коэффициентом прозрачности потенциального барьера называется величина
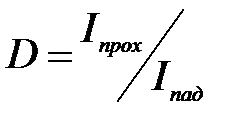. (5. 34)
Примерами туннельного эффекта могут служить выбрасывание a - частицы из ядра радиоактивного атома; переход электрона из металла в вакуум.
|
|
|
Коэффициент прозрачности прямоугольного потенциального барьера:
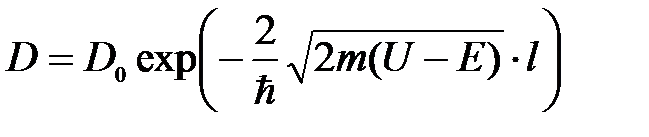, (5. 35)
где D – коэффициент прозрачности потенциального барьера; D0 – постоянный коэффициент, близкий к единице; m – масса частицы; Е – энергия частицы; l – ширина барьера; U – высота барьера, т. е. значение потенциальной энергии.
Коэффициент прозрачности барьера сложной формы:
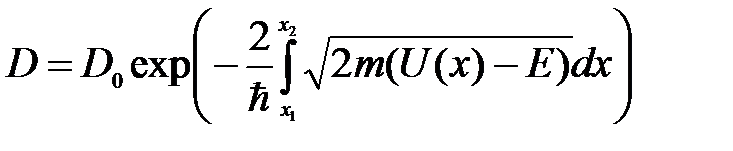, (5. 36)
где x1 и x2 – координаты начала и конца барьера; U(x) – значение потенциальной энергии для данного значения полной энергии Е.
Линейный гармонический осциллятор
Линейный гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Данная модель часто используется во многих задачах классической и квантовой теории. Так, примерами классических гармонических осцилляторов являются пружинный, физический и математический маятники. Потенциальная энергия гармонического осциллятора равна:
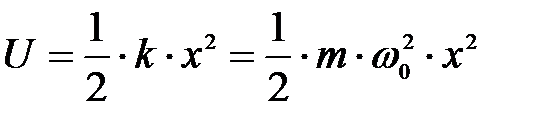, (5. 37)
где k – коэффициент жесткости системы; x – отклонение от положения равновесия; w0 – собственная частота колебаний осциллятора; m – масса колеблющейся системы.
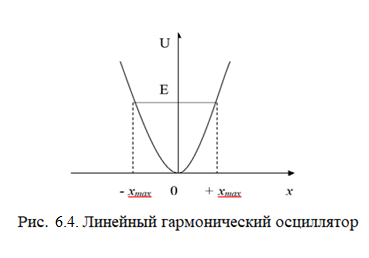Зависимость потенциальной энергии осциллятора от координаты U(x) имеет вид «ямы» с параболическими стенками (рис. 5. 4).
Амплитуда колебаний осциллятора определяется его полной энергией. В точках ± xmax полная энергия равна потенциальной, поэтому с классической точки зрения частица не может выйти за пределы области (от - xmax до + xmax ).
Гармонический осциллятор в квантовой механике описывается стационарным уравнением Шредингера, с учетом вида потенциального поля (5. 37):
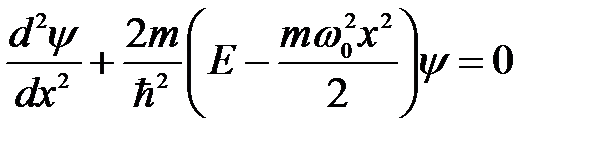. (5. 38)
Уравнение (5. 38) имеет решение только при собственных значениях энергии:
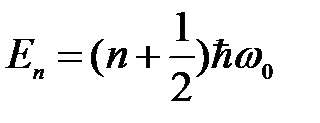(n = 1, 2, 3…. ). (5. 39)
Выражение (5. 39) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. энергия квантуется, причем существует минимальная энергия квантового гармонического осциллятора
|
|
|
. (5. 40)
Энергия (5. 40) называется энергией нулевых колебаний. Она определяется только собственной частотой осциллятора, ее невозможно отнять у осциллятора никаким охлаждением, она сохранилась бы и при Т = 0 К. Нулевой энергии соответствуют нулевые колебания гармонического осциллятора. Это значит, что частица не может находится на дне «потенциальной ямы». Из соотношения (5. 40) следует, что уровни энергии линейного гармонического осциллятора расположены равномерно, то есть, расстояния между соседними уровнями одинаковы и равны:
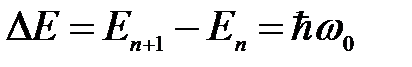. (5. 41)
То, что минимальная энергия квантового осциллятора не равна нулю (частица не может находиться на дне потенциальной ямы) связано с принципом неопределенности. Если бы энергия частицы была равна нулю, то частица покоилась бы, и ее импульс и координаты имели бы одновременно определенные значения, что противоречит принципу неопределенности. Наличие нулевой энергии квантового осциллятора подтверждается экспериментально.
Расчеты, выходящие за рамки уравнения Шредингера, показывают, что для квантового осциллятора возможны переходы лишь между соседними стационарными уровнями, при которых квантовое число изменяется на единицу: ∆ n = ± 1. При каждом из этих переходов испускается или поглощается квант энергии ћν .
|
|
|
