 |
Тема 4: «Корпускулярно-волновой дуализм свойств вещества. Волны де Бройля. Соотношение неопределенностей».
|
|
|
|
Тема 4: «Корпускулярно-волновой дуализм свойств вещества. Волны де Бройля. Соотношение неопределенностей».
Краткая теория
Корпускулярно-волновая природа микрочастиц
Де Бройль пришел к выводу, что классическая механика должна быть предельным случаем более общей механики, которую следует назвать волновой механикой или квантовой механикой.
Согласно де Бройлю, движение микрочастиц сопоставляется с некоторыми волнами. Их называют дебройлевскими волнами, или иначе волнами материи. Дебройлевская длина волны частиц с импульсом p:
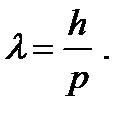(4. 1)
Эта формула справедлива для скоростей, много меньших скорости света. Таким образом, если частицы движутся около препятствий или проходит сквозь щели диафрагмы, размеры которых сравнимы с длиной дебройлевской волны, они будут вести себя так же, как ведут себя в аналогичных условиях волны.
Известные опыты Девиссона и Джермера с пучком электронов, рассеиваемых на решетке кристалла, блестяще подтвердила правильность предположений де Бройля.
Соотношение неопределенностей
Двойственная природа микрочастиц математически выражается в так называемых соотношениях неопределенностей, сформулированных в 1927 г. В. Гейзенбергом. Соотношения неопределенностей для координат и импульсов имеют вид:
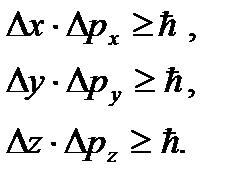(4. 2)
для энергии и времени:
(4. 3)
Соотношение (4. 3) логически вытекает из хорошо известной в теории колебаний связи, существующей между длительностью сигнала Dt и полосой частот Dw:
(4. 4)
|
|
|
Поскольку для микрочастиц справедлива формула
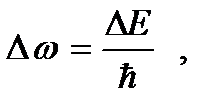(4. 5)
то, очевидно, можно написать, что
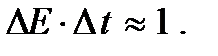(4. 6)
Соотношения неопределенностей для координат и импульсов также вытекают из известной классической формулы, связывающей ширину волнового пакета Dx с разбросом волновых чисел Dkx:
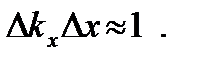(4. 7)
Таким образом, если признать справедливыми приведенные выше классические закономерности, а также два фундаментальных постулата квантовой теории (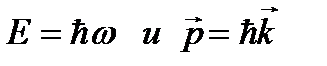 
), то соотношения неопределенностей получаются из них, как прямое следствие.
Сущность соотношения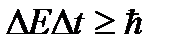 
может быть определена следующим образом: погрешность измерения энергии 
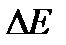определяется интервалом времени 
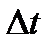, в течение которого может быть произведено данное измерение.
Сущность соотношений неопределенностей состоит в том, что невозможно одновременно точно определить координаты (x, y, z) и соответствующие проекции импульса (px, py, pz). Причем, это не связано с несовершенством методов измерения, а определяется двойственной корпускулярно-волновой природой микрообъектов.
Примеры решения задач
Задача 1. Электрон прошел ускоряющую разность потенциалов 51 В. Найти длину волны де Бройля для электрона.
| Дано: U = 51 В |
| lБ -? |
Решение:
Запишем формулу де Бройля:
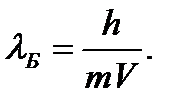
Пройдя ускоряющую разность потенциалов, электрон приобрел кинетическую энергию (нерелятивистский случай):
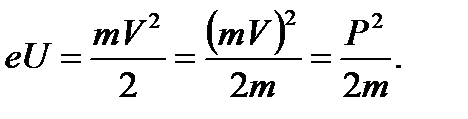
Отсюда выразим импульс электрона и запишем выражение для длины волны де Бройля:
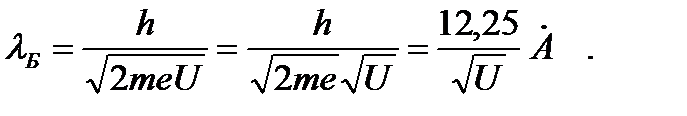
Вычислим длину волны де Бройля:
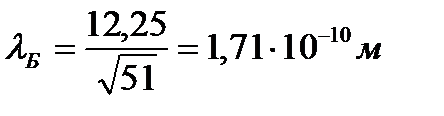
Ответ: λ Б = 1, 71 Å
Задача 2. Вычислите дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ.
| Дано: Wk = 100 эВ | СИ: 1. 6× 10-17 Дж |
| lБ -? |
Решение
|
|
|
Кинетическая энергия нерелятивистских частиц определяется выражением
.
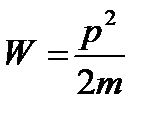Откуда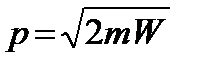 
.
Дебройлевская длина волны электрона
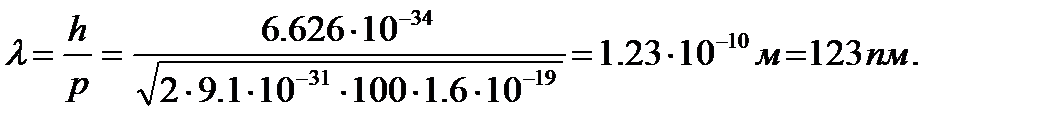
Дебройлевская длина волны протона
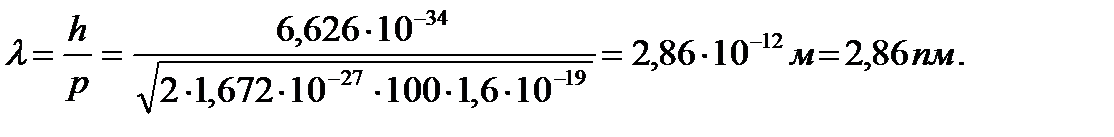
Дебройлевская длина волны атома урана:
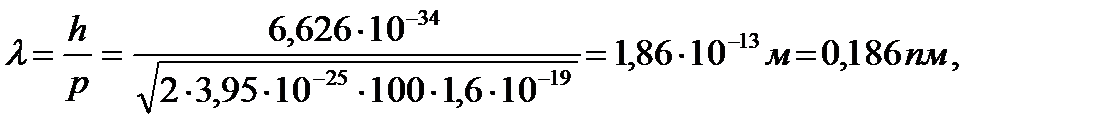
где масса атома урана
|
|
|
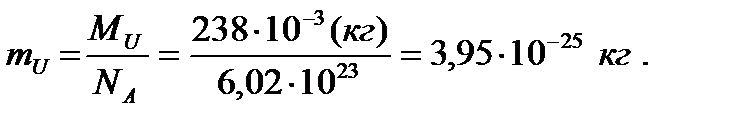
