 |
1.11.4. Контроль сложения на основе остатков по мод 3
|
|
|
|
1. 11. 4. Контроль сложения на основе остатков по мод 3
Идея этого способа состоит в том, что каждому слагаемому ставится в соответствие некоторый контрольный код, который представляет собой остаток этого числа по модулю 3. Одновременно с суммированием, выполняется суммирование контрольных кодов, которое позволяет обнаружить ошибку (это же относится и к любой другой арифметической операции).
S = A+B; A + B = 3 ( a + b ) + R (A) + R (B) (1. 14)
R(A) – остаток числа А по мод 3.
R(A) – остаток числа В по мод 3.
A = a × 3 + R (A)
B = b × 3 + R (B) a, b - целые числа или 0
R ( A+B ) = R (A) + R (B) = g × 3 + R [ R (A) + R (B) ], где
R (A) и R(B) Î { 0, 1, 2 }, g Î { 0, 1 }, R (A) + R (B) = [0.. 4] подставив в (9. 6) получим A + B = 3 (a + b + g ) + R [ R)A) + R(B) ] и
R ( A+B ) = R [ R)A) + R(B) ] (1. 15)
Соотношение (1. 15) является математическим решением задачи контроля и на ее основе строится логическая схема контроля.
Из теории известно, что контроль по модулю 3 обнаруживает все одиночные и часть двойных ошибок.
1. 11. 5. Формирование остатка двоичного числа по модулю 3
Рассмотрим двоичное число А2, ½ A½ > 1
A= an× 2n + an-1× 2n-1 + …+ a1× 21 + a0× 20
От этого двоичного числа перейдем к четверичному числу:
A = am × 4m + am-1 × 4m-1 + …+ a1 × 41 + a0 × 40
Каждая четверичная цифра числа получается из 2-х разрядов двоичного числа.
m = (n+1) /2 при ``n`` нечетном и m = n/2 при ``n`` четном
am = an× 2 + an-1 a0= a1× 2 + a0
am-1 = an-2× 2 + an-3 (1. 16)
Пример:
2120 2120 2120 2120
A2 = 1 0 1 1 0 1 0 1 = 18110
43 42 41 40
Цифры двоичного числа А разбиты на пары, которые соответствуют четверичным цифрам. Над двоичными цифрами каждой пары проставлены их двоичные веса, чтобы было легче определить четверичные цифры.
|
|
|
A4 = 2 × 43 + 3 × 42 +1 × 41 +1 × 40 = 128 + 48 + 4 + 1 = 18110
R (A) = R (am× 4m ) + R (am-1× 4m-1 ) +… + R (ai× 4i) + R (a0 )
так как остаток от суммы равен сумме остатков слагаемых, разложим бином 4i в ряд:
4i = ( 3 + 1 )i = 3i + C1× 3 i-1 + C2× 3 i-2 + …+ Ci-1× 3 + 1
где C1, C2, …Ci-1 – биномиальные коэффициенты,
R (4i) = 1 – остаток по модулю 3 величины 4i, тогда
R (A) = R (am) + R (am-1) +… + R (a1) + R (a0 )
R (A) = R (am +am-1 +… + a1 + a0 )
Остаток по модулю 3 некоторого числа А равен остатку суммы его четвертичных цифр.
Вычислим остаток по мод3 двоичного числа:
А2 = 0 1 1 0 1 1 0 1 1 0.
Пользуясь соотношениями (1. 16), переведем его в четверичный код:
А4 = 1 2 3 1 2 - четверичное число.
Преобразуем это число, заменив каждую цифру остатком по мод 3:
RI(A) = ( 1 2 0 1 2 ) – остаток по мод 3 каждой четверичной цифры числа А (остаток под мод 3 первого ранга).
RII(A) = ( 1 2 0 ) – попарное суммирование цифр остатков по мод 3 первого ранга (остаток второго ранга).
RIII(A) = ( 1 2 ) – результат попарного суммирования цифр предыдущего остатка (остаток третьего ранга).
RIV(A) =0 – окончательная сумма по мод 3 двоичного числа А2.
Проанализировав процесс формирования остатка по мод 3, найдем логические выражения на основании которых можно построить соответствующую логическую схему ( операция сложения заменяется логической операцией).
Таблица 1. 8
| a1 | a0 | a | R|(a) |
Запишем в таблице истинности (табл. 1. 8) правила перехода от пары двоичных цифр ``a1a0`` к четверичной цифре ``a0`` и к остатку R(a0).
Запишем формальные выражения
a0: = если (a1 & a0 ) то 3, иначе
если (a1 &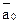 
) то 2, иначе
если (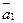 
& a0) то 1, иначе
если ( 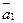& 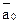) то 0;
RI (a0): = если ( 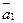& 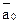) Ú (a1 & a0 ) то 0, иначе
если (a1 & 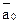) то 2, иначе (1. 9. )
|
|
|
если ( 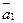& a0) то 1.
Выражение (1. 9. ) представляет собой логические правила формирования не только любой цифры остатка по мод 3 1-го ранга, но является справедливым и для получения цифр остатков всех последующих рангов. Как следует из примера и табл. 1. 8, формирование каждой цифры остатка следующего ранга происходит из соответствующей пары цифр предыдущего ранга. Каждая их этих цифр может иметь одно из трех значений: 0, 1, 2.
Таблица 1. 9.
| RI(i) | RI(i-1) | RII(j) |
В соответствии с этими соображениями составим таблицу истинности (табл. 9. 3), в которой отображена логическая зависимость между парой цифр остатка 1-го ранга и соответствующей цифрой остатка по мод 3 2-го ранга. Добавим, что эта таблица справедлива и для формирования цифр остатков последующих рангов.
На основании этой таблицы можно составить логические выражения для формирования остатков 2-го уровня и построить логические схемы.
Способ контроля правильности выполнения операции сложения на основе остатков по модулю 3 достаточно сложен, но применяется, если нужно обеспечить очень высокую достоверность вычислений.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Имеется некоторое десятичное число А= − 0. 75. Преобразовать в двоичный код и записать в двоичном формате для │ А│ < 1.
2. Записать целое десятичное число В= − 346 в двоичном формате для │ А│ > 1.
3. Записать десятичное число А= 437∙ 10-3 в двоичном коде в формате с плавающей точкой в нормализованном виде.
4. Преобразовать десятичное число В= − 0. 43 в двоичный код и записать в прямом, обратном и дополнительном кодах.
5. Преобразовать десятичные числа (простые дроби) А= 31/32, В= 17/64 в двоичный код и выполнить операцию вычитания по алгоритмам ПП, ПО, ПД.
6. Выполнить операцию вычитания для чисел А, В из пункта 5 по алгоритмам ДД, ОО.
7. Для десятичных чисел А=57939, В=27405 выполнить операцию сложения в двоично-десятичном коде 8421.
8. Для десятичных чисел А=57939, В=27405 выполнить операцию вычитания в двоично-десятичном коде 8421 по алгоритму ПД.
9. Для двоичных чисел А=0. 0110101 В=0. 11011101 выполнить операцию сложение с контролем на основе остатков по модулю 2.
|
|
|
10. Сформировать остаток двоичного числа по модулю 3 для чисел А1=101100010111 и А2= 110111001011.
|
|
|
