 |
Типовой расчет по теории игр. Тема: кооперативное решение.
|
|
|
|
Условия задачи.
Экономика состоит из двух агентов, совершающих добровольный обмен на наборах из двух товаров A и B. Функции полезности 1 и 2 агентов заданы уравнениями
, 
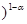, где 
- количество товара A у агента i, 
- количество товара B у агента i. Суммарные количества товаров A и B ограничены: 
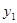
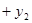
, где 
- положительные константы. Первоначально 1 агент владеет товарами A и B в количествах 
соответственно, причем 
. Агент 2 владеет оставшимися количествами товаров. Агенты вступают в добровольный обмен, увеличивающий их полезности. Решениями называются наборы товаров, поступающих в распоряжения каждого из агентов после обмена. Предполагается, что трансакционные издержки равны нулю, информация агентов совершенна.
Задание.
1. В модели Эджворта найти контрактную кривую, точку угрозы, переговорное множество;
2. В системе координат 
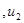найти уравнение, связывающее полезности агентов для решений, оптимальных по Парето;
3. В той же системе координат построить кривую оптимальных по Парето решений, найти точку угрозы, переговорное множество;
4. Найти арбитражное решение (решение Нэша);
5. Найти количества товаров A и B, которыми должны владеть агенты согласно арбитражному решению;
6. Показать, что для любого решения, не лежащего на контрактной кривой, найдется другое решение, которое эффективнее по Парето, чем первое.
Указание. Значения констант для каждого из 10 вариантов приведены в следующей таблице в соответствующей строке.
| № варианта | α | a | b | k1 | k2 | x0 | y0 |
| 1/3 | |||||||
| 2/3 | |||||||
| 1/2 | |||||||
| 1/4 | |||||||
| 1/2 | |||||||
| 1/3 | |||||||
| 2/3 | |||||||
| 1/2 | |||||||
| 1/4 | |||||||
| 1/2 |
Творческая часть задания. Ответьте на вопросы:
|
|
|
1. Пусть 1й агент имеет преимущество в переговорной силе, т.е. может диктовать свои условия. Каким в этом случае будет решение игры?
2. Чему при этом будут равны полезности агентов?
3. Почему в этом случае 2му агенту выгоднее принять условия, которые диктует 1 агент, чем оставаться в начальном положении?
4. Почему агент, имеющий преимущество в переговорной силе, не может захватить все ресурсы в условиях добровольного обмена?
5. Влияет ли соотношение переговорных сил агентов на арбитражное решение?
Литература
1. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.: МГУ им. М.В. Ломоносова, Издательство "ДИС", 1998. – 368 с.
2. Розен В.В. Математические модели принятия решений в экономике. Учебное пособие. – М.: Книжный дом "Университет", Высшая школа, 2002. – 288 с.
3. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр – М.: "Наука", 1981.
4. Нейман, Джон фон, Моргенштерн, Оскар Теория игр и экономическое поведение. – М.: "Наука"., 1970.
5. Вилкас Э.Й. Оптимальность в играх и решениях. – М.: Наука. 1990
6. Оуэн.Г. Теория игр. – М.: Мир, 1971.
7. Мулен. Э. Теория игр с примерами из математической экономики. – М.: Мир., 1985.
8. Гермейер Ю.Б. Игры с непротивоположными интересами. – М.: "Наука", 1976.
9. Жуковский В.И. Кооперативные игры и их приложения./Под ред. В.С. Молоствова. – М.: Эдиториал УРСС, 1990.
10. Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций: Учебник. – М.: Издательско-торговая корпорация "Дашков и К0", 2007. – 880 с.
11. Интриллигатор М. Математические методы оптимизации и экономическая теория. М.: Айрис-пресс, 2002.
12. Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заля. Вся высшая математика Теория вероятностей. Математическая статистика. Теория игр. Том(часть) 5.: Учебник - 3-е изд.,исправл. М.: ЛКИ, 2007. – 296с.
|
|
|
Учебное издание
Е.М.Скаржинская
А.С.Илюхина
К.С.Метелькова
"ТЕОРИЯ ИГР ДЛЯ ЭКОНОМИСТОВ "
УЧЕБНОЕ ПОСОБИЕ ПО ДИСЦИПЛИНЕ
Подписано в печать
Формат 60х90 1/16
Уч.-изд.л.
Тираж
Изд. № 28
КГУ имени Н.А.Некрасова
156961, г.Кострома, ул. 1 Мая,14
[1] Как мы убедимся позднее, оптимальными стратегиями в этом примере являются доминирующие стратегии.
[2] Парето, Вильфредо (Pareto, Vilfredo) (1848–1923), итальянский экономист и социолог, представитель математической школы в экономике. Парето известен т.н. «законом Парето», описывающим процесс распределения доходов, а также понятием оптимальности по Парето, применяемым в теории игр, микроэкономике и социологии.
[3] Бертран, Жозеф Луи Франсуа (1822-1900), французский математик, иностранный член-корреспондент (1859) и иностранный почетный член (1896) Петербургской АН. Труды по математическому анализу, теории групп. Конкуренция по Бертрану даже в условиях олигополии приводит к тому, что равновесная цена оказывается равной предельным издержкам каждого из дуополистов. (Это имеет место только в условиях совершенной конкуренции).
[4] См. Пиндайк Роберт С., Рубинфельд Дэниел Л. Микроэкономика: Пер. с англ. – М.: Дело, 2000, С. 544-545.
[5] Там же, С. 545-546
[6] Курно, Антуан Огюстен (Cournot, Antoine Augustin) (1801–1877), французский экономист, философ и математик. Курно был первым автором, который дал определение функции спроса и начертил ее график. Курно также был первым экономистом, разработавшим модели монополии и дуополии.
[7], где n – количество участников игры, – полезность i -го игрока, – полезность i -го игрока в точке угрозы.
|
|
|
