 |
4. REPRESENTATION
|
|
|
|
4. 1 BLOCK DIAGRAM
If a given system is a complicated one (like our example from the last chapter), it is very difficult to analyze the system as a whole. For such Control systems, we can find the transfer function of each and every element of the system. And by showing connection between the elements, the complete system can be split into different blocks and analyzed conveniently.
In block diagram representation, the interconnection of system components to form a system can be conveniently shown by the blocks arranged in proper sequence. It explains the cause and effect relationship existing between the input and output of the system, through the blocks. Each block in a block diagram is called a Functional block, it means the block explains the mathematical operation on the input by the element to produce the corresponding output. The transfer function of the element is mentioned inside the block.
There are four basic components of a block diagram. First are the blocks themselves describing the relation between input and output through transfer function. Then there are summing points, where the output of two or more blocks are added algebraically. The third component of a block diagram is called a take-off point, which represent the application of total output from a point as the input to some other block. Finally block diagrams contain arrows indicating the direction of flow of signals.

Utilizing some basic rules, it is possible to reduce a complex block diagram to a simple form. We shall discuss those rules and later then try out an example:
1. Combining Cascade blocks
Blocks connected in cascade can be replaced by a single block with transfer function equal to the product of the respective transfer functions.

2. Eliminating a Feedback loop
The transfer function of a simple feedback loop with, where G(s) is the forward path transfer function and H(s) is the feedback path transfer function, is given by


This can be easily proved as follows:

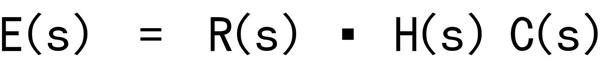


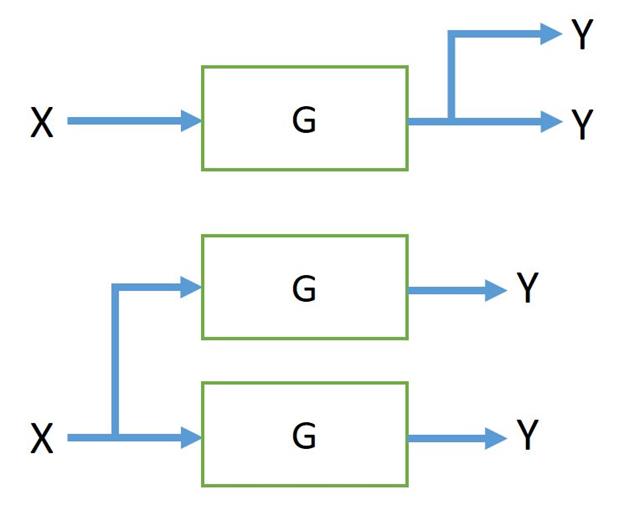
3. Parallel Blocks
Blocks are said to be in parallel if they have a common input and the overall output is the sum of the individual outputs. The overall transfer function is simply the sum of the transfer functions of the individual blocks

4. Moving a summing point ahead of a block
It is sometimes necessary to move a summing point ahead of a block to simplify the block diagram. This can be done provided the transfer function of the blocks are modified accordingly.

5. Moving a summing point behind a block

6. Moving a pick-off point behind a block

7. Moving a pick-off point ahead of a block
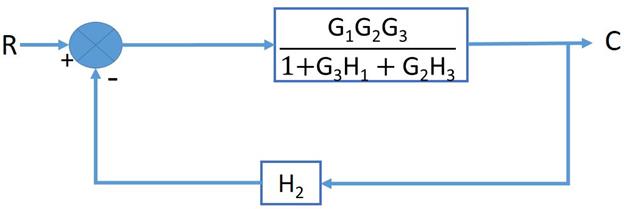
Example:
Let’s solve this example using the block diagram reduction technique. Keep in mind that it is not necessary to reduce the block in this exact same manner. Nonetheless the final answer will the same.
|
|
|



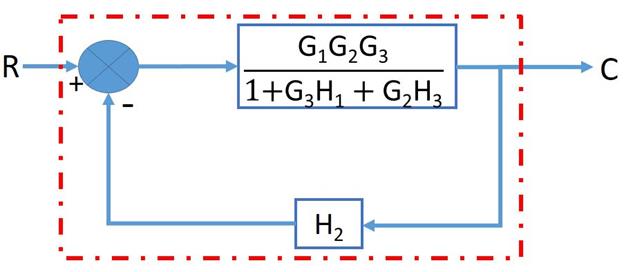
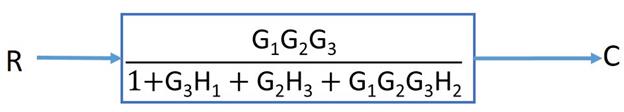
4. 2 SIGNAL FLOW GRAPHS
Signal flow graphs are an alternate way of representing systems, particularly when the set of equations describing the system are available. Unlike block diagrams, which consist of blocks, arrows, summing junctions, and pickoff points, a signal-flow graph consists only of branches, which represent systems, and nodes, which represent signals. In the signal flow graph, all the variables, dependent and independent are represented by small circles called Nodes. The relationships between various nodes are represented by joining the nodes as per the equations. The lines joining the nodes are called branches. Each branch is associated with a transfer function and an arrow. The transfer function represents the relationship between adjoining variables and the arrow indicates the direction of flow of signals.
Example:

4. 3 MASON’S RULE
If the block diagram is an extremely complicated one, it may take a while to find the transfer function using block reduction technique and most times it’s not worth the effort. Instead the transfer function of a block diagram can be obtained directly by using the Mason’s Gain formula. Although the Mason’s Gain formula was first developed as a method to solve signal flow graphs, it can be used with Block diagrams as well.
There are a few terms that you need to be familiar with before using this method.
1. Forward Path: is a path from the input node to the output node. In our example from above there are 2 forward paths.
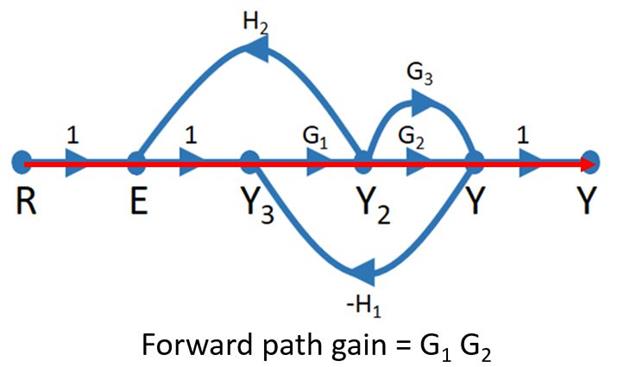

The forward path gain can be obtained by simply multiplying all the transfer functions along the path.
2. Loop: A loop is a path which originates from a node and terminates at the same node, without passing through any node twice. There are three loops in our example.
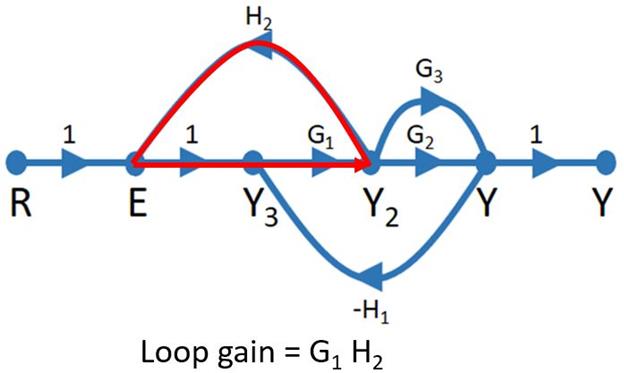
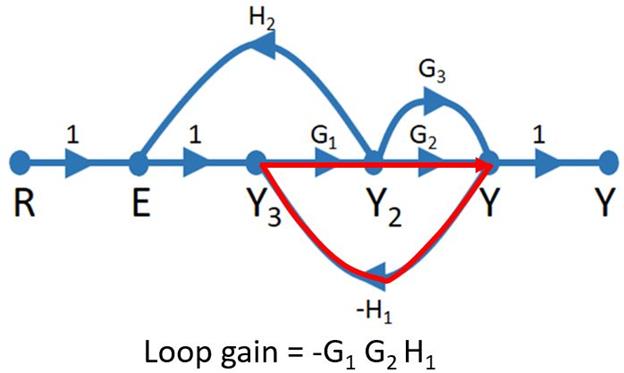

Loops that contain only one node are called self-loops. The loop gains can be obtained by multiplying the transfer functions of all the branches in the loop.
3. Non touching Loops: Loops that do not share a node are called non touching loops. There are no non touching loops in our example.
OK! Now that you are familiar with these basic concepts, let’s try and use the Mason gain formula to obtain the transfer function of the system in our example.
The first step in using the Mason’s gain formula is to identify all the possible forward paths and loops in the system. Then find the forward path gains and the loop gains for all the identified forward paths and loops. Denote the forward path gains as P1, P2, P3 etc. and the loop gains as L1, L2, L3 etc.
The next step is to identify the non-touching loops (if there are any) and then calculate the gain product of all possible combinations of two non-touching loops. In our example there are no 2 non-touching loops.
The Mason’s Gain formula is given by,

In our example,

As we saw with our example, the Mason’s Gain formula is a far easier method to find the overall transfer functions of system. All there is to do to identify the forward paths and loops correctly.
|
|
|


