 |
AppendIX. References
|
|
|
|
APPENDIX
1. FOURIER SERIES
Fourier series is a basic mathematical tool for representing periodic signals. Using Fourier series, it is possible to express periodic signals in terms of carefully chosen sinusoids. So every periodic signal in this world can be expressed used some combination of sinusoids. Isn't this cool??
In the above figure, notice how a series of sinusoids (sine and cosine waves) combine to form the resultant signal, which looks nothing like a sinusoid. (Note that the different components have different amplitudes and different frequencies)
The General expression for Fourier series is:
here a0, a1, a2..., b1, b2, b3.... are the Fourier coefficients. They tell us how much a sine or cosine wave of a particular frequency is contributing to the resultant signal.
The value of a0 tells us how much a cosine of zero frequency (cos 0 =1, so basically DC) is present in the final wave. a0 is also called the DC value or the Average value or the DC offset. Since all the other terms in the expansion are pure sinusoids, their individually average to zero, so the average value solely depends on a0.
Since sin 0 = 0, there can't be any contribution from zero frequency sine wave, so b0 is always 0.
The value of a1 tells us how much a cosine of fundamental frequency is present in the final wave.
Similarly, contribution from each sinusoid in the main signal can be found out separately. This information is very useful and it can be used to manipulate signals in a lot of ways.
Fourier series can be expressed in a more compact form using complex notation. Using the complex notation, we can represent the contributions from both sine and cosine waves of the same frequency by a single coefficient.
This is called the synthesis equation. Here the Fourier coefficients are complex. This notation has its advantages, it is possible to calculate all Fourier coefficients using a single expression. Electrical engineers use j instead of i, since i is frequently used to denote electric current.
The values of cn can be obtained using the expression:
This expression is called the analysis equation and the plot of |cn| vs n is called the frequency spectrum of the signal.
Notice the lines corresponding to each frequency component in the above picture. This is exactly the Frequency spectrum. It tells us how much each frequency component contributes to the original signal. This information is invaluable to us.
2. FOURIER TRANSFORM
We have now seen how the Fourier series is used to represent a periodic function by a discrete sum of complex exponentials. But how often are natural signals periodic?? Now that's a problem. Too bad we can't apply Fourier series to non periodic signals.
Why don't we assume an Aperiodic signal to be a periodic signal with infinite time period. Why don't we assume that the same pattern exists after infinite time. This is where we introduce the Fourier transform.
|
|
|
The Fourier transform is used to represent a general, non periodic function by a continuous superposition or integral of complex exponentials. The Fourier transform can be viewed as the limit of the Fourier series of a function when the period approaches to infinity, so the limits of integration change from one period to (− ∞, ∞ ).
The expression for the Fourier Transform is given by:
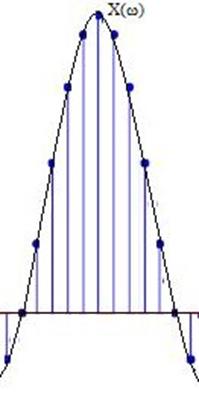
X(ω ) is a continuous function of ω. The Fourier series coefficients are basically the sampled values of X(ω ) or in other words, X(ω ) forms the envelope for the Fourier series coefficients.
REFERENCES
Advanced Engineering Mathematics by Erwin Kreyszig
The Scientist and Engineer's and Guide to Digital Signal Processing by Steven W. Smith.
Control Systems engineering by Norman S. Nice
Matlab Documentation http: //in. mathworks. com/help/ident/ref/bode. html
Discovering the Laplace Transform in Undergraduate Differential Equations by Terrance J. Quinn and Sanjay Rai
Youtube Channel by Brian Douglas https: //www. youtube. com/channel/UCq0imsn84ShAe9PBOFnoIrg? ab_channel=BrianDouglas
CONTACT
http: //beyondwhyy. me/
https: //twitter. com/beyondwhyy
beyondwhyy@gmail. com
|
|
|
