 |
6. STABILITY
|
|
|
|
6. 1 INTRODUCTION
What is stability?? The dictionary defines Stability as the ability of a substance to remain unchanged over time under stated or reasonably expected conditions of storage and use. This is actually a very good general definition. A system is said to be stable, if it does not exhibit large changes in its output for a small change in its input.
Before we dig into the stability of Control systems, let’s consider 2 practical cases to have a clear idea on the concept of stability.
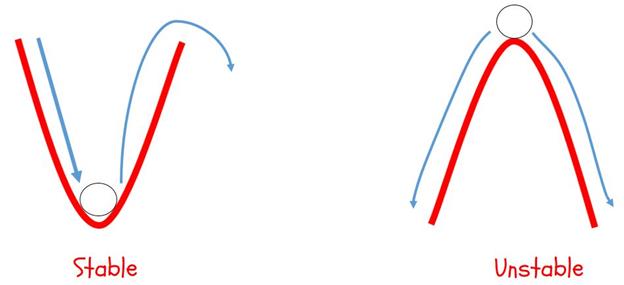
In the first example, a ball is placed in a u-shaped container. If we apply a small force on the ball, it moves back and forth slightly, but ultimately returns to its original position. Such a system is called a Stable system. Do keep in mind that if the force is larger than a certain threshold value, then the ball will not return to its original position. In the second example, the ball is placed on top on a hill, with slope on either side. In this case, the smallest disturbance will make the ball roll down the hill. Such a system is called an Unstable system.
6. 2 STABILITY OF CONTROL SYSTEMS
As we have seen in the previous chapter, every system has to pass through a definite transient period. Will the system reach the desired steady state value after passing through the transients successfully?? The answer to this question is the basis of stability analysis.
Knowing that an unstable closed-loop system is generally of no practical value, we seek methods to help us analyze and design stable systems. To determine the stability of a Control system, we use a concept called BIBO stability. BIBO stability stands for bounded input, bounded output stability. BIBO stability is the system property that any bounded input yields a bounded output. This is to say that as long as we input a signal with absolute value less than some constant, we are guaranteed to have an output with absolute value less than some other constant. In order to understand this concept, we must first look more closely into exactly what we mean by bounded. A bounded signal is any signal which in which the absolute value of the signal is never greater than some value. Since this value is arbitrary, what we mean is that at no point can the signal tend to infinity, including the end behavior. The Unit impulse is the bounded signal of choice to determine the stability of a system.
Mathematically, a system is said to be BIBO stable if,
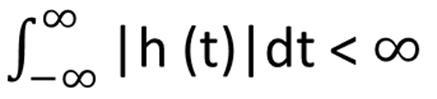
Where h(t) is the Unit impulse response.
Although stability can be determined this way. It is much easier to infer the stability of the system from the pole zero plot of the transfer function. The stability of a linear closed loop system depends on the location of the closed loop poles in the s-plane. For stable systems, all poles must be to the left of the imaginary axis.
Let’s look at an example to prove this:
In the above example, the pole at s=2 corresponds to the term e2t in the step response. As t 
, this term itself tends to 
, not allowing the response to settle down to a steady state value, making the system unstable. If any of the poles of the system lies on the imaginary axis, then the system is said to be marginally stable, meaning the response will keep on oscillating without either settling down or tending to infinity.
|
|
|
6. 3 ROUTH-HURWITZ CRITERION
The Routh–Hurwitz stability criterion is a mathematical method of determining the location of poles of the system (with respect to imaginary axis) without actually solving the equation. In order to find the close loop poles of a system, we equate the denominator of the closed-loop transfer function to zero. The equation so obtained is called the Characteristic equation of the system. In the example we considered in the previous section, the closed loop transfer function was given in a convenient form, so we had no problem in determining the closed loop poles directly. The general form of the Characteristic equation is,
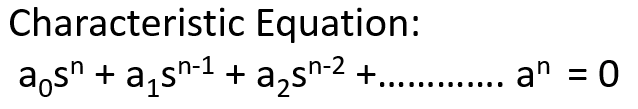
There are two parts to this criterion: The necessary condition and the sufficient condition.
Necessary Condition
1. All the coefficients should be real and positive.
2. All the coefficients should be non-zero.
If any of these conditions fail, then the system is Unstable. But do keep in mind that these conditions do not guarantee the stability of the system, for that we need to check the sufficient conditions
Sufficient Condition
To check these conditions, we need to construct a Routh array.
The first row will consist of all the even terms of the characteristic equation. The second row will consist of all the odd terms of the characteristic equation.
The elements of third row can be calculated as:
The elements of fourth row can be calculated by multiplying the terms of the second and third row in a similar way. The process is continued till coefficient for s0 is obtained
The necessary and sufficient condition for stability is: All the terms in the first column of the Routh array must have same sign. If any sign change exists, then the system is unstable and the number of sign changes is equal to the number of roots lying in the right half of s-plane.
Looks tough right?? Not really, it looks sort of messy and confusing because we have stated the criterion as a set of rules. But you are one example away from getting grip of this whole thing.
6. 4 SPECIAL CASES OF ROUTH HURWITZ CRITERION
1. First element of a row is zero and rest of the row contains at least one non-zero element:
In such cases, a small positive number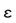 
is substituted in place of zero, then the array is completed using 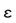. Then examine the sign change by taking 
.
2. All the elements of a row in the array are zero:
This is a slightly more trickier situation than the previous one. To eliminate this difficulty, an equation is formed by using the coefficients of the row just above the concerned row. Such an equation is called the auxiliary equation.
Then the derivative of the Auxiliary equation with respect to s is taken and the coefficients of that equation are used to replace the row of zeros. Now complete the array in terms of these new terms.
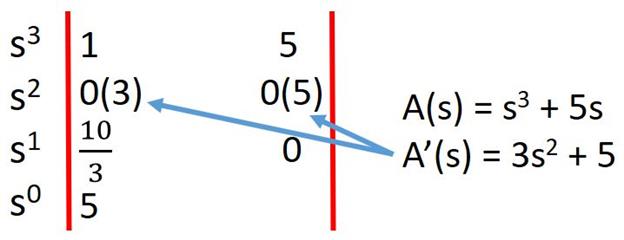
After completing the Routh array, all we need to do is to check for the sign change in the first row (below the replaced row). If there are any sign changes, that means that the system is unstable. If there is no sign change, the system may be stable. To confirm stability, you need to solve the Auxiliary equation and make sure that the roots doesn’t lie on the imaginary axis.
|
|
|
6. 5 AUXILIARY EQUATION
The auxiliary equation is actually a part of the characteristic equation, which means that the roots of the auxiliary equation are also the roots of the characteristic equation. The other interesting thing is that the roots of the auxiliary equation are the most dominant roots of the characteristic equation. This allows us to determine the stability of the system directly from the roots of the Auxiliary equation. The other roots of the characteristic are always in the left half plane and do not play any significant role in stability analysis. This is why we check for sign changes only below the Auxiliary equation.
Properties of Auxiliary Equation
1. The roots of the Auxiliary equation are always symmetrical about the y-axis.
2. No. of roots on the imaginary axis = Order of the AE – 2 x (No. of sign changes below AE).
|
|
|
