 |
Методы решения нелинейных уравнений
|
|
|
|
Руководитель
(подпись) (дата)
Студент
(подпись) (дата)
2009
Содержание
Введение
1. Постановка задачи
2. Методы решения нелинейных уравнений
2.1 Общие сведения
2.2 Метод касательных (метод Ньютона)
2.2.1 Общие сведения
2.2.2 Решение нелинейного уравнения методом касательных
2.3 Метод хорд
2.3.1 Общие сведения
2.3.2 Решение нелинейного уравнения методом хорд
2.4 Вывод
2.5 Метод простых итераций
2.5.1 Общие сведения
2.5.2 Решение нелинейного уравнения методом простых итераций
2.6 Программа для решения нелинейных уравнений
3. Решение нелинейных уравнений методом интерполирования
3.1 Интерполяция
3.2 Многочлен Лагранжа
3.3 Интерполяция сплайнами
3.4 Использование интерполяции на практике
3.4.1 Интерполяция с помощью многочлена Лагранжа
3.4.2 Обратная интерполяция
3.4.3 Интерполяция сплайнами
3.5 Программа для использования интерполяции
4. Итерационные методы решения систем линейных алгебраических уравнений
4.1 Общие сведения
4.2 Метод простой итерации
4.2.1 Описание метода
4.2.2 Решение СЛАУ методом простых итераций
4.2.3 Программа для решения СЛАУ методом простых итераций
4.3 Метод Зейделя
4.3.1 Описание метода
4.3.2 Решение СЛАУ методом Зейделя
4.3.3 Программа дл решения СЛАУ методом Зейделя
4.4 Сравнительный анализ
5. Сравнительный анализ различных методов численного дифференцирования и интегрирования
5.1 Методы численного дифференцирования
5.1.1 Описание метода
5.1.2 Нахождение производной
5.2 Методы численного интегрирования
5.2.1 Общие сведения
5.2.2 Нахождение определенного интеграла
5.3 Решение ОДУ
5.3.1 Решение ОДУ методом Эйлера
5.3.2 Решение ОДУ методом Рунге-Кутты
6.Численные методы решения обыкновенных дифференциальных уравнений
|
|
|
6.1 Общие сведения
6.2 Метод Эйлера
Заключение
Список использованной литературы
Введение
На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит главным образом не потому, что мы не умеем этого сделать, а поскольку искомое решение обычно не выражается в привычных для нас элементарных или других известных функциях. Поэтому важное значение приобрели численные методы, особенно в связи с возрастанием роли математических методов в различных областях науки и техники и с появлением высокопроизводительных ЭВМ.
Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ.
В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.
Конечно, использование таких программных продуктов значительно сокращает время и ресурсы по решению ряда важных задач. Однако, использование этих программ без тщательного анализа метода, с помощью которого решается задача, нельзя гарантировать, что задача решена правильно. Поэтому для более полного понимания того, как осуществляется расчет различного вида уравнений и их систем, необходимо теоретически изучить методы их решения и на практике их проработать.
Целью выполнения данного курсового проекта является приобретение практических навыков решения нелинейных уравнений, системы линейных алгебраических уравнений, обыкновенных дифференциальных уравнений различными численными методами.
Постановка задачи
Порядок выполнения:
По итерационным методам решения нелинейных уравнений:
Определить корень в заданном или любом выбранном отрезке методом хорд, касательных, простых итераций.
|
|
|
Используя результаты решений, указать наименьший полученный отрезок, в котором содержится корень уравнения.
Для каждого метода и каждой задачи построить график функции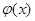 
на [ a, b] и убедиться в выполнении условия сходимости итерационной процедуры.
Используя функции f (x) из п.1, построить интерполяционный многочлен L4 (x) на [ a, b], использовав в качестве узловых a и b, остальные необходимые узловые точки выбрать, разделив промежуток [ a, b] на почти равные части. Вычислить значения f (x) и L4 (x) в двух точках, одна из которых - середина крайней части, а вторая - середина части, содержащей точку 
. Сравнить полученные величины. Используя эти же узловые точки, провести обратную интерполяцию и определить значение х при y=0. Полученный результат сравнить с ранее найденным решением уравнения.
Сравнить результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации.
Провести сравнительный анализ различных методов численного дифференцирования и интегрирования.
Найти численное решение обыкновенного дифференциального уравнения методом Эйлера и уточненным методом Эйлера с 5-ю и 20-ю шагами и сравнить их, если возможно с результатом точного решения ОДУ.
Методы решения нелинейных уравнений
Общие сведения
Рассмотрим уравнение вида f (x) =0, (2.1), где f (x) - любая нелинейная функция.
Корнем уравнения ( 2.1) называется значение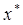 
, при котором 
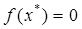. Способы приближенного решения, т.е. алгоритм решения, предполагает определение x* c некоторой наперед заданной точностью.
Для нахождения корней уравнения (2.1) различают следующие два этапа.
Отделения (локализации) корней, т.е. нахождение таких интервалов по аргументу x, внутри каждого из которых существует только один корень уравнения (2.1). Если у функции на концах исследуемого отрезка [a,b] функция имеет разные знаки, то на этом отрезке функция имеет не менее одного корня. Если же одинаковые знаки, то функция может не иметь корней или иметь четное число корней. Следовательно, локализация заключается в том, что необходимо установить отрезки, на которых есть смена знаков функции и, кроме того, выполнено условие единственности корня, т.е. функция на этом отрезке должна иметь первую производную с постоянным знаком. Из условия сходимости итерационной последовательности также требуется, чтобы вторая производная не меняла знак, т.е. на исследуемом отрезке функция бала бы только выпуклой или вогнутой.
|
|
|
Уточнение корней заключается в применении некоторого итерационного метода, в результате которого корень уравнения (2.1) может быть получен с любой наперед заданной точностью ε. При этом, останавливая процесс на какой-либо конечной итерации, необходимо оценить погрешность по сравнению с точным корнем, который неизвестен. Выбранный метод позволяет построить последовательность х1, х2, х3, …, хk, … приближений к корню. Итерационный процесс состоит в последовательном уточнении начального приближения х0. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х1, х2, х3, …, хk, … Если эти значения с ростом k стремятся к истинному значению корня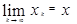 
, то итерационный процесс сходится.
Основными методами решения нелинейных уравнений, реализованных в виде численной процедуры, являются итерационные методы.
|
|
|
