 |
Решение нелинейного уравнения методом касательных
|
|
|
|
1. Дано уравнение tg (0.36*x +0.4) =x2. Решить его методом касательных с точностью решения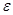 
=0,001.
Для нахождения корня исследуем функцию
.
График функции представлен на рисунке 2.2
Рисунок 2.2 - График исследуемой функции
Находим отрезок, в котором функция монотонно возрастает или убывает, а также где концы отрезка будут иметь разные знаки.
Выбираем концы отрезка: a= -1; b = 0. График функции на этом отрезке представлен на рисунке 2.3
Рисунок 2.3 - График функции на выбранном отрезке
Проверяем существование корня на отрезке по условию 
f (-1) = - 0,95998
f (0) =0,42279
0,405869<0, следовательно, на данном промежутке корень есть.
Исследуем функцию на монотонность: 
Экстремумов на выбранном отрезке нет.
Находим первую производную функции:
В точке a первая и вторая производные равны:
, 
В точке bпервая и вторая производные равны:
, 
Выбираем тот конец отрезка, который совпадает со знаком 2-ой производной.
, x0=-1, 
-0,95998* (
) =1,90998; 
По формуле
находим:
, 
, 
x>0.001
x>0.001
x>0.001
, 
x<0.001
Необходимая точность достигнута при n=4, т.е. на 4-й итерации.
Так как заданная точность достигнута, то процесс можно прекратить.
Теперь строим график функции x= 
, т.е. последовательность xn, стремящаяся к x* и условием сходимости здесь является 
(рисунок 2.4).
Рисунок 2.4 - График функции для исследуемой функции
2. Дано уравнение
x3-0,2x2+0,4x-1,4=0.
Решить его методом касательных с точностью решения 
=0,001.
Для нахождения корня исследуем функцию
.
График функции представлен на рисунке 2.5
Рисунок 2.5 - График исследуемой функции
|
|
|
Находим отрезок, в котором функция монотонно возрастает или убывает, а также где концы отрезка будут иметь разные знаки.
Выбираем концы отрезка: a= -0.1; b = 1.5 График функции на этом отрезке представлен на рисунке 2.6
Рисунок 2.6 - График функции на выбранном отрезке
Проверяем существование корня на отрезке по условию
-3,066375
3,066375 <0, следовательно, на данном промежутке корень есть.
Исследуем функцию на монотонность:
6,2225>0
Экстремумов на выбранном отрезке нет.
Находим первую производную функции:
; 
В точке a первая и вторая производные равны:
, 
В точке bпервая и вторая производные равны:
, 
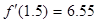Выбираем тот конец отрезка, значение функции в котором совпадает со знаком 2-ой производной.
Принимаем:
x0= 1,5 
2.125*6.55=13,91875, 
По формуле
находим:
x>0.001
x>0.001
x>0.001
x<0.001
Необходимая точность достигнута при n=4, т.е. на 4-й итерации.
Так как заданная точность достигнута, то процесс можно прекратить.
Теперь строим график функции x= 
, т.е. последовательность xn, стремящаяся к x* и условием сходимости здесь является (рисунок 2.7).
Рисунок 2.7 - График функции 
для исследуемой функции
Метод хорд
Общие сведения
Как и в методе хорд, функция f (x) должна удовлетворять на отрезке [a, b] следующим условиям:
1) существование производных 1-го и 2-го порядков;
2) f ’ (x) 
0;
3) производные 1-го и 2-го порядков знакопостоянны на отрезке [a, b].
За начальное приближение x0 принимается один из концов отрезка [a, b], где значение функции имеет такой же знак, что и 2-я производная. За x1 выбирается второй край отрезка. В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются значения х0, х1,… точек пересечения хорды с осью абсцисс (рисунок 2.8).
Рисунок 2.8 - Метод хорд
|
|
|
Формула для n-го приближения имеет вид:
Итерационный процесс останавливают при выполнении условия 
; где ε - заданная точность.
|
|
|
