 |
Решение нелинейного уравнения методом хорд
|
|
|
|
1. Дано уравнение
tg (0.36*x +0.4) =x2.
Решить его методом хорд с точностью решения 
=0,001.
Как в предыдущем методе для нахождения корня исследуем функцию
.
Выбираем концы отрезка: a= -1; b = 0. График функции на этом отрезке представлен на рисунке 2.9
Рисунок 2.9 - График функции на выбранном отрезке
По данным из п.2.2.2 за x0 выбираем тот конец отрезка, который совпадает со знаком 2-ой производной. А за x1 второй конец отрезка.
x0=-1; x1=0.
По формуле
находим:
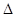x>0.001
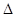x>0.001
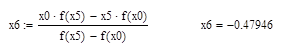
x>0.001
x>0.001
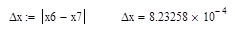
x>0.001
x<0.001
Необходимая точность достигнута при n=7, т.е. на 6-й итерации.
Так как заданная точность достигнута, то процесс можно прекратить.
Теперь строим график функции x= 
, т.е. последовательность xn, стремящаяся к x* и условием сходимости здесь является 
(рисунок 2.10).
Рисунок 2.10 - График функции для исследуемой функции
2. Дано уравнение x3-0,2x2+0,4x-1,4=0. Решить его методом хорд с точностью решения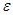 
=0,001.
Как в предыдущем методе для нахождения корня исследуем функцию
.
График функции представлен на рисунке 2.5
Выбираем концы отрезка: a= -0.1; b = 1.5 График функции на этом отрезке представлен на рисунке 2.11
Рисунок 2.11 - График функции на выбранном отрезке.
По данным из п.2.2.2 за x0 выбираем тот конец отрезка, который совпадает со знаком 2-ой производной и удовлетворяет условию 
. А за x1 второй конец отрезка.
x0=1,5; x1=0,5.
По формуле
находим:
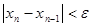
x>0.001
x>0.001
x>0.001
x>0.001
x>0.001
x>0.001
x>0.001
x<0.001
Необходимая точность достигнута при n=9, т.е. на 8-й итерации.
Так как заданная точность достигнута, то процесс можно прекратить.
|
|
|
Теперь строим график функции x= , т.е. последовательность xn, стремящаяся к x* и условием сходимости здесь является 
(рисунок 2.12).
Рисунок 2.12 - График функции для исследуемой функции.
Вывод
Судя по графикам и сравнивая эти два метода, можно сделать вывод, что искомый корень находится в промежутке между найденными приближенными корнями, т.е. для функции 
на отрезке [-0.48059; - 0.48028], а для для функции 
на отрезке [1,0627; 1,06289]
На рисунках 2.12, 2.13 приведены графики функций на данных отрезках.
Рисунок 2.12 - График функции 
Рисунок 2.13 - График функции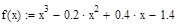 
Анализируя эти два метода, можно отметить, что в методе хорд, чтобы достичь заданной точности, необходимо выполнять больше итераций, чем в методе касательных. Так, в первом примере, в методе хорд мы выполнили 6 итераций, а в методе касательных всего 4; во втором примере в методе хорд мы выполнили 8 итераций, а в методе касательных всего 4. С другой стороны, в методе хорд не нужно вычислять производную функции на каждом шаге. Таким образом, как мне кажется, метод касательных является более трудоемким.
Метод простых итераций
Общие сведения
Пусть дано уравнение f (x) =0, (1)
Метод простых итераций уточнения корней уравнения (1) состоит в замене этого уравнения эквивалентным ему уравнением
(2)
и построении последовательности
(3),
где
,
Например
x0 = (а + b) /2
Если не удается выразить х из уравнения (1), то эквивалентное уравнение и эквивалентную функцию можно построить, например, так:
Последовательность (3) называют методом простых итераций уточнения корней уравнения (1).
Теорема (достаточное условие сходимости метода простых итераций). Пусть функция 
в эквивалентном уравнении ( 2) определена и дифференцируема на отрезке 
Тогда, если существует число q такое, что
|
|
|
но отрезке [а, b], то последовательность ( 3) сходится к единственному корню уравнения ( 2) при любом начальном приближении x0.
Критерий окончания итерационного процесса. При заданной точности 
>0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство
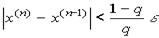
Если величина 
, то можно использовать более простой критерий окончания итераций:
|
|
|
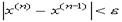
