 |
Решение СЛАУ методом простых итераций
|
|
|
|
Решить СЛАУ методом простых итераций с точностью  .
.

Для удобства преобразуем систему к виду:

Условие сходимости:
 ,
,

Принимаем приближение на 0-ом шаге:
 ,
, 
 ,
, 
На 1-м шаге выполняем следующее:
Подставляем принятые приближения в первоначальную систему уравнений




Смотрим не выполняется ли условие остановки итерационного процесса:
 :
:

На 2-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса
 :
: 
На 3-м шаге выполняем следующее:


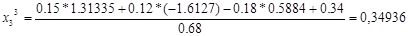

Смотрим не выполняется ли условие остановки итерационного процесса
 :
: 
На 4-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса
 :
: 
На 5-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса:
 :
: 
На 6-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса:
 :
: 
Необходимая точность достигнута на 6-й итерации. Таким образом, итерационный процесс можно прекратить.

Программа для решения СЛАУ методом простых итераций
На рисунке 4.1 представлена программа для решения систем алгебраических линейных уравнений методом простых итераций.
Листинг программы приведен в приложении Г.

Рисунок 4.1 - Программа "Метод простых итераций"
Метод Зейделя
Описание метода
В этом методе результаты, полученные на k-том шаге, используются на этом же шаге. На (k+1) - й итерации компоненты приближения  вычисляются по формулам:
вычисляются по формулам:
|
|
|


………………………………………….

Этот метод применим к система уравнений в виде Ax=B при условии, что диагональный элемент матрицы коэффициентов A по модулю должен быть больше, чем сумма модулей остальных элементов соответствующей строки (столбца).
Если данное условие выполнено, необходимо проследить, чтобы система была приведена к виду, удовлетворяющему решению методом простой итерации и выполнялось необходимое условие сходимости метода итераций:
 , либо
, либо 
Решение СЛАУ методом Зейделя
Решить СЛАУ методом Зейделя с точностью  .
.

Эту систему можно записать в виде:

В этой системе сразу видно, что выполняется условие, где диагональные элементы матрицы коэффициентов по модулю больше, чем сумма модулей остальных элементов соответствующей строки.
Для удобства преобразуем систему к виду:

Условие сходимости:
 ,
,

Принимаем приближение на 0-ом шаге:




На 1-м шаге выполняем следующее:
Подставляем принятые приближения в первоначальную систему уравнений




Смотрим не выполняется ли условие остановки итерационного процесса
 :
:

На 2-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса
 :
:

На 3-м шаге выполняем следующее:




Смотрим не выполняется ли условие остановки итерационного процесса:
 :
:

На 4-м шаге выполняем следующее:


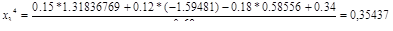

Смотрим не выполняется ли условие остановки итерационного процесса
 :
:

Необходимая точность достигнута на 4-й итерации. Таким образом, итерационный процесс можно прекратить.

Программа дл решения СЛАУ методом Зейделя
На рисунке 4.2 представлена программа для решения систем алгебраических линейных уравнений методом простых итераций.
|
|
|
Листинг программы приведен в приложении Г.

Рисунок 4.2 - Программа "Метод Зейделя"
Сравнительный анализ
Можно заметить, что в методе Зейделя быстрее мы достигаемой нужной точности, в нашем случае в точность была достигнута на 4-й итерации, когда в методе простых итераций она была достигнута на 6-й итерации. Но в то же время в методе Зейделя ставится больше условий. Поэтому вначале нужно произвести иногда довольно трудоемкие преобразования. В таблице 4.1 приведены результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации:
Таблица 4.1 - Результаты решения СЛАУ
| № шага | Метод постой итерации | Метод Зейделя |
| 0 | x1=1.34 x2=-1.75 x3=0.5 x4=0.65 | x1=1.34 x2=-1.75 x3=0.5 x4=0.65 |
| 1 | x1=1.277 x2=-1.56227 x3=0.3147 x4=0.5335 | x1=1.277 x2=-1.57047 x3=0.3324 x4=0.5837 |
| 2 | x1=1.31335 x2=-1.6127 x3=0.3647 x4=0.5884 | x1=1.32469 x2=-1.5974 x3=0.355808 x4=0.58638 |
| 3 | x1=1.315391 x2=-1.5935 x3=0.34936 x4=0.57867 | x1=1.318014 x2=-1.5945 x3=0.354137 x4=0.58556 |
| 4 | x1=1.3173416 x2=-1.5968 x3=0.35577 x4=0.58589 | x1=1.318367 x2=-1.59481 x3=0.35437 x4=0.58554 |
| 5 | x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 | |
| 6 | x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 |
|
|
|


