 |
Сравнительный анализ различных методов численного дифференцирования и интегрирования
|
|
|
|
Методы численного дифференцирования
Описание метода
Предположим, что в окрестности точки xi функция F (x) дифференцируема достаточное число раз. Исходя из определения производной:
Для оценки погрешностей формул численного дифференцирования используется формула Тейлора:
(1)
Отбрасывая последнее слагаемое, мы можем вычислить производную.
Тогда отброшенное слагаемое будет являться погрешностью в формуле (1). В зависимости от того, какая точка выбирается за x отличают правостороннюю и левостороннюю производную.
Если для вычисления 
вместо x возьмем xi-1, то получится левосторонняя производная (2), а если xi+1, правосторонняя производная (1).
(1)
(2)
Отсюда видно, что порядок погрешности x - xi, т.е. при использовании
xi-1 или xi+1, порядка O (h).
При достаточно очевидном результате выражения (1) и (2) имеют низкую точность, т.е. высокую погрешность. Поэтому на практике больше используются так называемая центрально-симметричная формула, имеющая большой порядок точности.
Очевидно, что эта формула используется только для внутренних точек отрезка.
Нахождение производной
Вычислим производную функции f (x) =sin (x) в какой-либо точке на отрезке [0,π] двумя способами.
Разобьем отрезок на части:
h= 
Найдем производную в точке x= 
.
По центрально-симметричной формуле:
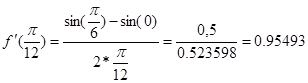
По формуле правосторонней производной:
=cos () =0.9659,
значит вычисление производной по центрально-симметричной формуле более точнее.
Методы численного интегрирования
Общие сведения
Для вычисления определённого интеграла используется формула:
|
|
|
Вычисление интеграла в таком виде не всегда удается, поэтому возникает задача приближенного значения этого интеграла.
В теории численного интегрирования используются следующие формулы для вычисления:
Формула левых прямоугольников:
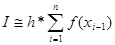
Формула правых прямоугольников:
У этих формул погрешность порядка О (h).
Улучшения результатов можно добиться путем интерполирования (интерполирование можно вести на отрезке [a,b]). Интерполяция первого и второго порядка носит
Формула трапеции:
Формула Симпсона
, где n=2m
h=b-a/n
Нахождение определенного интеграла
Вычислим интеграл для функции 
разными способами.
Разобьем отрезок [0, 
] на части:
h= 
По формуле левых прямоугольников:
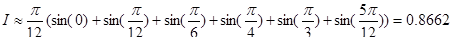
По формуле трапеции:
По формуле Симпсона:
При m=3:
При m=2:
Сравним полученные результаты с табличным:
=1
Можно сделать вывод, при вычислении определенного интеграла наибольшую степень точности дает формула Симпсона.
Решение ОДУ
Решение ОДУ методом Эйлера
, 
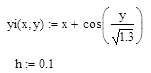Далее приведены результаты вычислений.
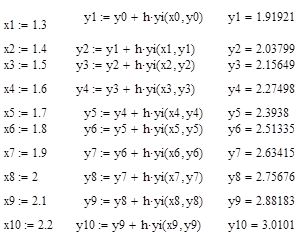
Далее приведены результаты вычислений.
Решение ОДУ методом Рунге-Кутты
, 
Далее приведены результаты вычислений.
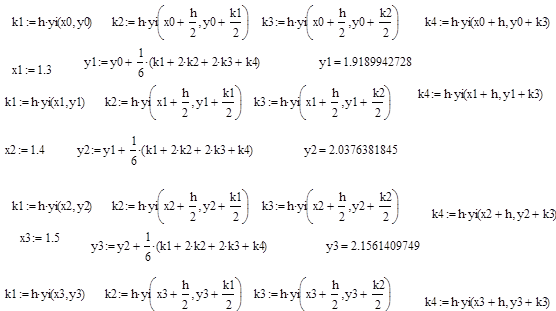
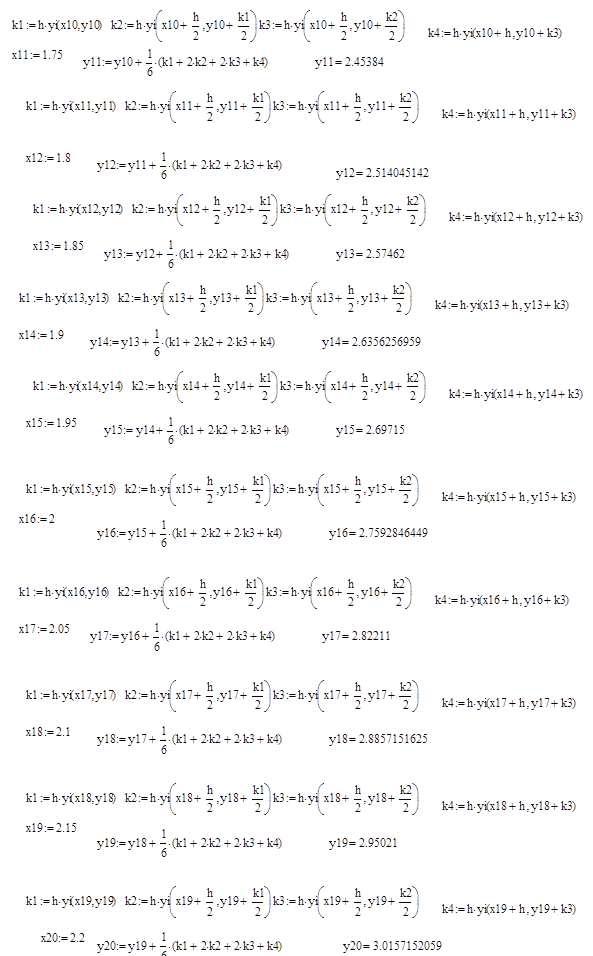
Поправка Ричардсона Ri для метода Эйлера:
Поправка Ричардсона Ri для метода Рунге-Кутта:
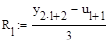
Численные методы решения обыкновенных дифференциальных уравнений
Общие сведения
Обыкновенные дифференциальные уравнения являются моделью динамических систем. То есть систем меняющих свои свойства при изменении независимой переменной в качестве таковой очень часто выступает время.
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y (x). Их можно записать в виде
|
|
|
,
где х - независимая переменная.
Наивысший порядок n входящей в уравнение
производной называется порядком дифференциального уравнения.
Методы решения обыкновенных дифференциальных уравнений можно разбить на следующие группы: графические, аналитические, приближенные и численные.
Графические методы используют геометрические построения.
Аналитические методы встречаются в курсе дифференциальных уравнений. Для уравнений первого порядка (с разделяющимися переменными, однородных, линейных и др.), а также для некоторых типов уравнений высших порядков (например, линейных с постоянными коэффициентами) удается получить решения в виде формул путем аналитических преобразований.
Приближенные методы используют различные упрощения самих уравнений путем обоснованного отбрасывания некоторых содержащихся в них членов, а также специальным выбором классов искомых функций.
Численные методы решения дифференциальных уравнений в настоящее время являются основным инструментом при исследовании научно-технических задач, описываемых дифференциальными уравнениями. При этом необходимо подчеркнуть, что данные методы особенно эффективны в сочетании с использованием современных компьютеров.
Существуют различные задачи для ОДУ, мы будем рассматривать задачу Коши. Из курса математики известны условия существования единственности решения задачи Коши и также известно, что аналитически эта задача решается в достаточно редких случаях. То есть для того чтобы ОДУ являлась моделью некоторого динамического процесса, имела аналитическое решение приходится принимать слишком много предположений упрощающих исходную постановку. Что далеко не всегда является продуктивным.
Метод Эйлера
Начальные условия: х=х0, у=у0, 
=f (x,y). Задача заключается в том, что необходимо построить функцию y=F (x) или Ф (х, у) =0, производная которой удовлетворяет заданному дифференциальному уравнению. Причем кривая соответствующей этой функции проходит через точку (х0, у0). Мы будем искать на заданном отрезке [a, b] х0=а значения некоторой функции, которые близки к соответствующим значениям искомого решения. Иногда говорят, что мы строим сеточную функцию, если разобьем отрезок [a, b] на n частей (h= (b-a) /n, где h - шаг сетки), тогда хi=x0+ih. Заменим в левой части производную правой разностью. При этом значения функции 
узлах 
заменим значениями сеточной функции 
:
|
|
|
Полученная аппроксимация ДУ имеет первый порядок, поскольку при замене 
на
допускается погрешность 
.
Будем считать для простоты узлы равноотстоящими, т.е.
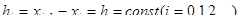
Тогда из равенства
Получаем
Заметим, что из уравнения 
следует
.
Поэтому
представляет собой приближенное нахождение значение функции 
в точке 
при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу. Полагая i=0, с помощью соотношения
находим значение сеточной функции 
при
: 
.
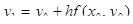Требуемое здесь значение 
задано начальным условием 
, т.е. 
. Аналогично могут быть найдены значения сеточной функции в других узлах:
Построенный алгоритм называется методом Эйлера, графически он представлен на рисунке 6.1.
Рисунок 6.1 -Метод Эйлера
Метод Рунге-Кутты
Одним из способов улучшения метода Эйлера является метод Рунге-Кутты. Формула Рунге - Кутты 4-го порядка:
, 
, 
, 
Заключение
В ходе выполнения курсовой работы был проведен сравнительный анализ численных методов, таких как итерация, интерполяция, численное дифференцирование и интегрирование, а также метод Эйлера.
В результаты все поставленные задачи были выполнены, цели достигнуты. Мы приобрели навыки в применении различных численных методов на практике. А также были исследованы различные методы.
Теперь перед нами стоит задача в применении приобретенных знаний в своей будущей профессиональной деятельности.
Список использованной литературы
1. Р.Ф. Хемминг "Численные методы (для научных работников и инженеров)". - Москва, 1972.
|
|
|
2. А.А. Амосов, А.Ю. Дубинский, Н.В. Копченова "Вычислительные методы для инженеров". - Москва, "Высшая школа", 1994.
3. Ф.В. Формалев, Д.Л. Ревизников "Численные методы". - М.: ФИЗМАТЛИТ, 2004.
4. Е.А. Волков. Численные методы: Учеб. Пособие для вузов - М.: Наука. Гл. ред. физ-мат. лит., 1987. - 248 с.
|
|
|
