Использование интерполяции на практике

 

Интерполяция с помощью многочлена Лагранжа

Задание: найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в неравносторонних узлах таблицы. Дана функция:

 

 

Составляем таблицу узлов интерполяции:

Поскольку n=5 строим интерполяционный многочлен L₅ (x):

 

L₅ (x) =P₅₀*f (x₀) +P₅₁*f (x₁) + P₅₂*f (x₂) + P₅₃*f (x₃) + P₅₄*f (x₄) + P₅₅*f (x₅)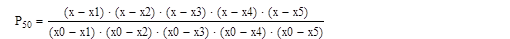

 

В результате получаем многочлен:

 

L₅ (x) = 1.049*10^-3*x⁵+5.4373*10^-3*x⁴ +0.027*x³ - 0,936*x² + 0,424*x +0.42278, X= - 0.48051

 

Подставляя заданное значение аргумента, получаем ответ:

 

L₅ (x) = 0,00011

 

При подстановки того аргумента в заданную функцию, получаем такой же результат:

 

f (-0.48051) =0.00011

 

Обратная интерполяция

 

Задание: найти приближенное значение корня данном значении функции с помощью интерполяционного многочлена Лагранжа, если функция задана в равносторонних узлах таблицы.

Дана функция:

 

 

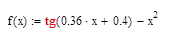
Составляем таблицу узлов интерполяции:

 

i	Xi	Yi
0	-0,7	-0.34091
1	-0,5	-0.02638
2	-0,3	0.21059
3	-0,1	0.37098
4	0,1	0.4559

 

Поскольку n=4 строим интерполяционный многочлен L₄ (y):

 

L₄ (y) =P₄₀*x₀+P₄₁*x₁+ P₄₂*x₂+ P₄₃*x₃+ P₄₄*x₄

 

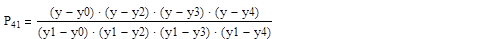
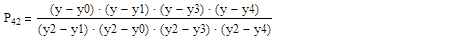
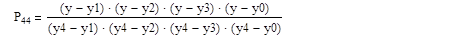
В результате получаем многочлен:

 

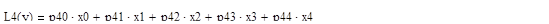
L₄ (y) = 7.99*y⁴-0.8176*y^{3 -} 0.4932* y² +0.9008*y - 0.4759

y= 0

 

Подставляя заданное значение функции, получаем ответ:

 

L₄ (y) = - 0.47591

 

Таким образом, получаем приближенное значение корня:

 

X= - 0.47591

 

При подстановки этого аргумента в заданную функцию, получаем результат:

 

f (-0,47591) = 0.00625

Интерполяция сплайнами

Задание:

На участке [b,b+2] выбрать 3 точки (b,b+1,b+2), построить два сплайна на двух отрезках, убедиться в том, что в точке b+1 производная не терпит разрыва.

 

 

Построим таблицу:

 

i	1	2	3
xi	0	1	2
yi	0.42279	-0.4955	-1.93404

 

 

Для построения сплайна используем формулы:

 

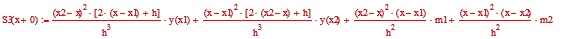
h=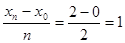

 

Таким образом, нам необходимо, чтобы вторая производная была непрерывна, т.е. получить сплайн с дефектом 1.

Для построения глобального сплайна необходимо, начиная со второго узла поставить условие непрерывности 2-ой производной, т.е.2-ая производная при подходе к точке 2 и дальше слева (x₁-0) должна равняться 2-ой производной при подходе справа (x₁+0):

 

 

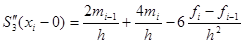
Приравнивая эти значения, получаем:

 

 

Для нашей функции получаем:

 

 0.42435

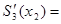 - 2.10346

 

После того, как мы нашли m₁, можем построить графики (рисунок 3.2).

S3(x1+0)

S3(x1 -0)

Рисунок 3.2 - Глобальная интерполяция сплайнами

 

Также можно сравнить с графиком самой функции (рисунок 3.3).

 

S3(x1+0)

F(x)

S3(x1 -0)

Рисунок 3.3 - Сравнение графика функции и глобальной интерполяции

 

Программа для использования интерполяции

 

На рисунках 3.4 представлена программа для использования интерполяции сплайнами. Пользователь вводит необходимые данные и при нажатии кнопки "График" строится кубический сплайн.

Листинг программы представлен в приложении В.

 

Рисунок 3.4 - Программа для использования интерполяции сплайнами

 

Итерационные методы решения систем линейных алгебраических уравнений

 

Общие сведения

 

К численным методам линейной алгебры относятся численные методы решения систем линейных алгебраических уравнений. Методы решения СЛАУ разбиваются на две группы. К первой группе принадлежат так называемые точные или прямые методы - алгоритм, позволяющий получить решение системы за конечное число арифметических действий. Вторую группу составляют приближенные методы, в частности итерационные методы решения СЛАУ.

 

Метод простой итерации

 

Описание метода

Рассмотрим СЛАУ вида

Ax = B, где А - матрица. (1)

 

A = {a_ij}i, j = 1…n

B = {b_i}x = {x_i}

 

Если эту систему удалось привести к виду x = Cx + D, то можно построить итерационную процедуру

 

x_k = Cx_k-1 + D

 

x_k → x*, где х* - решение заданной системы.

В конечном варианте система будет имееть вид:

 

x₁=c₁₁x₁+c₁₂x₂+c₁₃x₃+…c_1nx_n+d₁

x₂=c₂₁x₁+c₂₂x₂+c₂₃x₃+…c_2nx_n+d₁

x₃=c₃₁x₁+c₃₂x₂+c₃₃x₃+…c_1nx_n+d₃

_{…………………………………………..}

x_n=c_n1x₁+c_n2x₂+c_n3x₃+…c_nnx_n+d_n

 

Условием сходимости для матрицы С выполняется, если сумма модулей коэффициентов меньше единицы по строкам или по столбцам, т.е.

 

, или .

 

Необходимо, чтобы диагональные элементы матрицы А были ненулевыми.

Для преобразования системы можно выполнить следующие операции:

 

x₁₌a₁₁^-1 (c₁-a₁₂x₂ - a₁₃x₃-… - a_1nx_n)

x₂₌a₂₂^-1 (c₂-a₂₁x₂ - a₂₃x₃-… - a_2nx_n)

………………………..

x_n=a_nn^-1 (c_n-a_n1x₂ - a_n3x₃-… - a_n-1nx_n-1)

В результате получим систему:

x₁₌0+ c₁₂x₂+ c₁₃x₃-…+ c_1n-1x_n-1+ c_1nx_n+d₁

x₂₌ c₂₁x₂+0 +c₂₃x₃+…+ c_2n-1x_n-1+ c_2nx_n+d₂

_{………………………………………………………..}

x_n= c_n1x₁+ c_n2x₂ +c_n3x₃+…+ c_nn-1x_n-1+ 0+d_n

 

В ней на главной диагонали матрицы С находятся нулевые элементы, остальные элементы выражаются по формулам:

 

с_ij=-a_ij/a_ii, d_i=c_i/a_ii (i,j=1,2,3…n, i<>j)

 

Итерационный процесс продолжается до тех пор, пока значения х₁ ^(k), х₂ ^(k), х₃ ^(k) не станут близкими с заданной погрешностью к значениям х₁ ^(k-1), х₂ ^(k-1), х₃ ^(k-1).

 

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: