 |
1.3. Основной закон теплопроводности (Закон Фурье)
|
|
|
|
1. 3. Основной закон теплопроводности (Закон Фурье)
При процессе теплопроводности количество переданного тепла пропорционально температурному градиенту и площади сечения, перпендикулярного направлению распространения тепла:
, Вт.
Если же количество переданного тепла отнести к единице площади сечения и единице времени, то соотношение можно записать в виде:
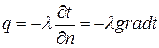, Вт/м2.
Это уравнение является математическим выражением основного закона распространения тепла путем теплопроводности – закона Фурье, на (Фурье Жан Батист Жозеф (1768-1830) франц. ученый) основе которого можно вывести расчетные формулы теплопроводности. Коэффициент 
характеризует собой способность вещества проводить тепло:
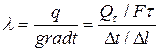, Вт/(м∙ К)
где 
- полное количество теплоты переданное за время 
.
Следовательно: коэффициент теплопроводности это количество тепла, которое проходит в секунду через один кв. метр поверхности, при падении температуры в один градус на один метр пути теплового потока.
Коэффициенты теплопроводности строительных и теплоизоляционных материалов имеют значения от 0, 023 до 2, 9 Вт/(м·К). Материалы с λ < 0, 25 Вт/(м∙ К) – применяют для тепловой изоляции и называют теплоизоляционными.
1. 4. Дифференциальное уравнение теплопроводности.
Дифференциальное уравнение теплопроводности Фурье
.
В уравнении множитель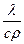 
называется коэффициентом температуропроводности и обозначается a.
Размерность коэффициента температуропроводности
= 
.
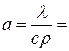
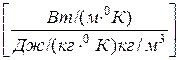или
,
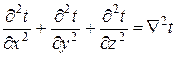где 
- выражение оператора Лапласа в декартовых координатах.
Дифференциальное уравнение теплопроводности Фурье обычно записывают в следующем виде
|
|
|
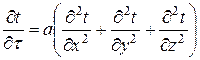
или
Дифференциальное уравнение теплопроводности устанавливает связь между временными и пространственными изменениями температуры в любой точке тела, в котором происходит процесс теплопроводности.
Коэффициент температуропроводности a является физическим параметром вещества, он существенен для нестационарных тепловых процессов и характеризует скорость изменения температуры. Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств вещества, т. к. скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности a.
Коэффициент температуропроводности зависит от природы вещества. Например жидкости и газы обладают большой тепловой инерционностью и следовательно малым коэффициентом температуропроводности. Металлы обладают малой тепловой инерционностью, так как они имеют большой коэффициент температуропроводности.
Если система имеет внутренние источники теплоты qv≠ 0, то выражение принимает вид
,
где 
- удельный тепловой поток внутреннего источника.
Дифференциальное уравнение теплопроводности дает возможность решать задачи, связанные с распространением тепла в теле (среде) теплопроводностью, как при установившемся, так и при неустановившемся тепловом потоке.
1. 5. Условия однозначности для процессов теплопроводности
Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно описывает явление теплопроводности в самом общем виде. Поэтому можно сказать, что это дифференциальное уравнение описывает целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса.
|
|
|
Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями.
Условия однозначности включают в себя:
- геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс;
- физические условия, характеризующие физические свойства среды и тела;
- временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени;
- граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.
Геометрическими условиями задаются формы и линейные размеры тела, в котором протекает процесс.
Физическими условиями задаются физические параметры тела (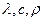 
и др. ) и может быть задан закон распределения внутренних источников тепла.
Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано (при τ =0); t=f(x, y, z).
При равномерном распределении температуры в теле начальное условие упрощается (при τ =0);
t=t0=const.
Граничные условия могут быть заданы несколькими способами.
Граничные условия первого рода. Задается распределение температуры на поверхности тела для каждого момента времени:
tс= f(x, y, z, τ ),
где tс – температура на поверхности тела; x, y, z – координаты поверхности тела.
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процессов теплообмена, уравнение упрощается и принимает вид:
tс= const.
Граничные условия второго рода. Задаются значения теплового потока для каждой точки поверхности тела и любого момента времени.
qn= f(x, y, z, τ ),
где qn – плотность теплового потока на поверхности тела; x, y, z – координаты.
В простейшем случае плотность теплового потока по поверхности и во времени остается постоянной
|
|
|
qn= q0= const.
Такой случай теплообмена имеет место, например при нагревании различных металлических изделий в высокотемпературных печах.
Граничные условия третьего рода. При этом задаются температура окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой. Граничное условие третьего рода характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тепла. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона-Рихмана.
Согласно закону Ньютона-Рихмана: количество теплоты, отдаваемое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела tс и окружающей среды tж (tс> tж)
q=α (tс- tж),
где α – коэффициент пропорциональности называемый коэффициентом теплоотдачи, Вт/(м2·К) характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.
Коэффициент теплоотдачи зависит от большого типа факторов. Однако во многих случаях его можно считать неизменным, и при решении задач теплопроводности будем принимать величину α постоянной.
Дифференциальное уравнение с заданными условиями однозначности дает полную математическую формулировку краевой задачи теплопроводности, которая разрешается аналитическими или экспериментальными методами.
|
|
|
