 |
6.1. Основные положения
|
|
|
|
Теплоотдачей называется конвективный теплообмен между твёрдым телом и движущейся средой (жидкостью или газом), который осуществляется совместным действием теплопроводности и конвекции при наличии температурного напора 
между телом и средой.
Коэффициент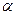 
характеризует интенсивность процесса теплоотдачи. Различают средний по всей поверхности теплообмена коэффициент теплоотдачи и местный (локальный), определяемый в заданной точке поверхности.
2. 1. Гидродинамический и тепловой пограничный слои
При течении среды на поверхностистенки образуется гидродинамический пограничный слой вязкой жидкости. В пределах этого слоя (по нормали к поверхности) скорость потока изменяется от нуля на поверхности до скоростиневозмущённого потокана внешнейгранице слоя. Движение жидкости впограничном слое может иметь ламинарный и турбулентный характер, а толщина слоя постепенновозрастает по направлению движения жидкости.
В условиях теплообмена наповерхности стенки образуется тепловой пограничный слой среды, в пределах которого температура теплоносителяизменяется от температурына стенке 
до температуры среды вдали от стенки 
.
В тонком слое жидкости па поверхности стенки (вязкий подслой) перенос теплоты осуществляется теплопроводностью: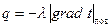 
, где значение градиента температуры жидкости 
определяется на поверхности тела.
Уравнениетеплоотдачи
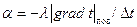(6. 1)
выражает связь между коэффициентомтеплоотдачи 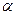, с однойстороны, и температурным полем вжидкости, а также ее теплопроводностью 
, с другой.
2. 2. Подобие и моделирование конвективного теплообмена
|
|
|
При экспериментальном изучении тепловых процессов принято выражать математическое описание процесса и расчетные уравнения в виде зависимостей между числами (критериями) подобия, представляющими собой безразмерные комплексы.
Уравнения подобия, выражая обобщенную зависимость между величинми, характеризующими процесс, справедливы для всех подобных между собой процессов. Первая теорема подобия: для подобных между собой процессов все одноименные числа подобия численно одинаковы, например Re==idem, Pr=idem. Согласно второй теореме подобия связь между числами подобия выражается в форме однозначной функциональной зависимости, например Nu=f(Re, Pr, Gr, ... ).
Третья теорема подобия утверждает, что условия подобия физических явлений, заключаются в подобии условий однозначности и равенстве одноименных чисел подобия, составленных из величин, входящих в| эти условия.
2. 3. Числа теплового и гидромеханического подобия процессов
Нуссельта число – безразмерный коэффициент теплоотдачи
, (5. 1)
где – коэффициент теплопроводность жидкости; l–характерный линейный размер.
Прандтля число – безразмерная характеристика теплофизических свойств жидкости
(5. 6)
где 
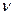и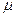 
– кинематическая, м2/с, и динамическая, Па·с, вязкости; 
и 
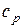–плотность, кг/м3, и изобарная массовая теплоемкость Дж/(кг·К), жидкости; а= 
– коэффициент температуропроводности жидкости, 
.
Пекле число – критерий теплового подобия
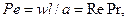(5. 7)
где Re – число Рейнольдса; w – характерная скорость потока, м/с
Стантона число – критерий вынужденного конвективного переноса теплоты
(5. 8)
Фурье число – критерий тепловой гомохронности
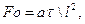(5. 9)
где 
– время протекания нестационарного процесса теплопроводности
|
|
|
Био число–критерий краевого подобия
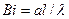(5. 10)
где l – характерный линейный размер твердого тела; –теплопроводность твердого тела.
Тепловой критерий фазового превращения
(5. 11)
где r –теплота испарения (конденсации), Дж/кг; –разность температур насыщения и перегрева (переохлаждения) фазы; 
–разность энтальпий фазы в состояниях насыщения и перегрева (переохлаждения).
Галилея число–критерий подобия полей свободного течения
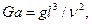(5. 12)
g – ускорение свободного падения, м/с2.
Грасгофа число – критерий свободной тепловой конвекции
(5. 13)
где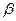 
– коэффициент объемного расширения, 
; для идеальных газов 
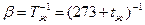; для капельных жидкостей приближенно 
, где 
и 
–плотности жидкости при и 
. Для воды 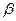-можно определить по табл. 3 приложения.
Релея число– критерий теплообмена при свободной конвекции
(5. 14)
Фруда число – критерий гравитационного подобия, характеризует меру отношения сил инерции и тяжести в потоке:
(5. 15)
Рейнольдса число – критерий режима движения жидкости
(5. 16)
Эйлера число- критерий подобия полей давления
(5. 17)
-перепад давления на участке движения жидкости.
Архимеда число – критерий свободной конвекции
(5. 18)
где 
–плотности жидкости в двух точках потока.
Определяющая температура, до которой выбираются теплофизические свойства жидкости или газа, входящие в числа подобия, указывается нижним индексом возле числа подобия: «ж», «с», «п. с»–соответственно средняя температура жидкости, стенки, пограничного слоя. Например,
(5. 19)
Определяющий геометрический размер также может быть указан нижним индексом возле числа подобия: l и h–длина и высота поверхности, d– диаметр трубы и т. п. Например,
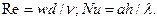(5. 20)
|
|
|
