 |
1.6.3.2. Цилиндрическая стенка с круглым ребром постоянной толщины
|
|
|
|
Расчет теплопередачи через трубу, оребренную снаружи кольцевыми ребрами (рис. 2. 3), можно проводить по формулам (2. 7) и(2. 8)принимая h=R–r и умножая коэффициент эффективности Е на поправочный коэффициент 
, который определяется по графику рис. (2, 1)
Коэффициент эффективности круглого ребра
(2. 1)
где – коэффициент, определяемый по графику рис. 2. 4 в зависимости от 
и R/r;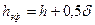 
- эффективная высота ребра, 
–отношение избыточных температур на конце у основания ребра.
Параметр m определяется из выражения
Рис. 2. 3. Круглое ребро постоянной толщины
Рис. 2. 4. Зависимость ε к=f(ϑ к/ϑ 0; R/r) для круглого ребра
1. 6. 4. Теплообмен с учетом внутренних источников теплоты
B определенных условиях в телах могут происходить процессы выделением (поглощением) теплоты, например джоулево нагревание электропроводника, химические экзо- и эндотермические реакции, ядерные процессы в тепловыделяющих элементах (твэлах) реактора и т. п. |и процессы характеризуются мощностью внутренних источников теплоты или интенсивностью объемного тепловыделения
, Вт/м3.
1. 6. 4. 1. Однородная неограниченная пластина. Для плоской пластины ( 
=const), равномерно охлаждаемой обеих сторон (рис. 3. 1), задана температура поверхности 
.
Рис. 3. 1. Температурный график в пластине с учетом внутренних источников теплоты
Одномерное температурное поле пластине толщиной 2 
(3. 1)
где 
В формуле (3. 1) при х=0 температура в середине толщины пластины
(3. 2)
Учитывая зависимость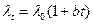 
в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле
|
|
|
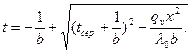(3. 3)
Для плоской пластины ( =const), равномерно охлаждаемой с обеих сторон, заданы температура среды 
и коэффициент теплоотдачи а.
Одномерное температурное поле в пластине
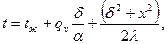(3. 4)
где
В формуле (3. 4):
при х= температура на поверхности пластины
(3. 5)
при х=0 температура в середине толщины пластины
(3. 6)
Мощность внутренних источников теплоты для пластины опреде| ляется по формулам
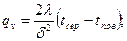(3. 7)
(3. 8)
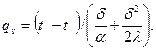(3. 9)
Связь между объемной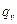 
и поверхностной 
плотностями тепло выделения используется при определении теплового потока на боковых поверхностях пластины
(3. 10)
1. 6. 4. 2. Цилиндрический стержень.
Розглянемо круглий циліндр (мал. 1), радіус якого малий але порівнянню з довжиною циліндра. При цих умовах температура буде змінюватися тільки уздовж радіуса.
Внутрішні джерела теплоти рівномірно розподілені по обсязі тіла. Задано температуру навколишнього середовища tж = const і постійний по всій поверхні коефіцієнт тепловіддачі. При цих умовах температура у всіх крапках зовнішньої поверхні циліндра буде однакова.
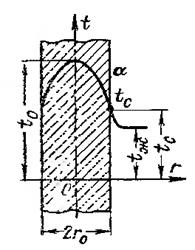
Рис. 1. Теплопровідність однорідного циліндричного стрижня при наявності внутрішніх джерел теплоти
Длябесконечного стержня( =const) задана температура на оси 
.
Температурное поле в стержне диаметром 
(3. 11)
В формуле (3. 8) при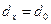 
температура на поверхности стержня
(3. 12)
С учетом зависимости 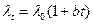температурное поле в стержне
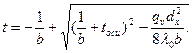(3. 13)
Для стержня ( =const), равномерно охлаждаемого средой, заданы ее температура и коэффициент теплоотдачи а.
|
|
|
Температурное поле в стержне
(3. 14)
В формуле (3. 14):
при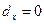 
температура на оси стержня
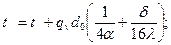(3. 15)
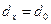температура на поверхности стержня
(3. 16)
Мощность внутренних источников теплоты для стержня
(3. 17)
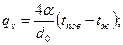(3. 18)
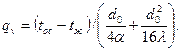(3. 19)
1. 6. 4. 3. Теплообмен в условиях электрического нагрева
При прохождении электрического тока по проводнику цилиндрической формы диаметром do и длиной l температуры рассчитываются формулам (3. 12) и (3. 15), в которых 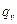выражается через электрические параметры: I–силу тока, A; U–напряжение, В; 
–электрическое сопротивление проводника, Ом:
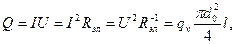(3. 30)
где 
–удельное электрическое сопротивление материала проводника, Ом·м.
1. 7. Теплопроводность при нестационарном режиме
Нестационарная теплопроводность характеризуется изменениемтемпературного поля тела во времени и связана с изменением энтальпии тела при его нагреве или охлаждении. Безразмерная температура тела 
определяется с помощью числа Био Bi=al/ , числа Фурье Fо =а 
/ 
и безразмерной координаты, обозначаемой для пластины X=х/ , а для цилиндра R= 
. Охлаждение (нагревание) тел происходит в среде с постоянной температурой , при постоянном коэффициенте теплоотдачи а; , и а – теплопроводность и температуропроводность материала тела, l–характерный размер тела ( 
для пластины, 
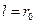для цилиндра), х и r–текущие координаты соответственно для пластины и цилиндра.
1. 7. 1. Тела с одномерным температурным полем
Пластина толщиной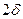 
. Безразмерная температура пластины
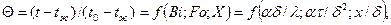(4. 1)
где t-температура в пластине для момента времени в точке с координатой х; 
– температура пластины в начальный момент времени..
Если Fo> 0, 3, то температура на поверхности пластины (Х=1)
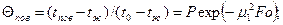(4. 2)
Температура на середине толщины пластины (Х=0)
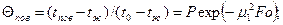(4. 3)
Температура внутри пластины на расстоянии х от ее средней плоскости
(4. 4)
где 
определяются по табл. 5 приложения для пластины в зависимости от числа Bi.
Температура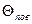 
и 
можно определить по графикам рис. П. 1, П. 2 по известным числам Bi и Fo.
|
|
|
Цилиндр радиусом 
. Безразмерная температура цилиндра
(4. 15)
где t–искомая температура в цилиндре для радиуса 
и времени .
Если Fo> 0, 3, то температура на поверхности цилиндра (R=1)
(4. 6)
Температура на оси цилиндра (R=0)
(4. 7)
Температура внутри цилиндра для радиуса
(4. 8)
где 
определяются по табл. 6 приложения для цилиндра в зависимости от числа Bi; 
–функция Бесселя первого рода нулевого порядка (табл. 19 приложения).
Температуры 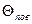и 
можно определить по графикам рис. П. 3, П. 4 Приложения по известным числам Bi и Fo.
1. 7. 2. Тела конечных размеров. Температура определяется на основе теоремы о перемножении решений: безразмерная температура тела конечных размеров при нагревании (охлаждении) равна произведению безразмерных температур тел с бесконечным размером, при пересечении которых образовано данное конечное тело.
Цилиндр длиной 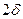и радиусом (рис. 4. 1). Он образован пересечением бесконечной пластины толщиной 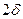и бесконечного цилиндра радиусом .
Безразмерная температуры стержня 
равна
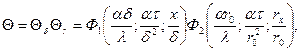(4. 9)
Рис. 4. 1. Цилиндрический стержень длиной l=2δ и радиусом r0
где 
(или функция 
) при Fo> 0, 3 определяется по формулам (4. 1)–(4. 3) и графикам рис. П. 1 и П. 2 приложения для бесконечна пластины толщиной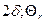 
(или функция 02) при Fo> 0, 3 определяется по формулам (4. 5)–(4. 7) и графикам рис. П. З и П. 4 приложения для бесконечного цилиндрического стержня радиусом .
При Fo> 0, 3 безразмерная температура внутри цилиндрического стержня в точке с координатами х и будет определяться аналоги но, но 
рассчитывается по формуле (4. 4), a 
–по формуле (4. 4) с использованием табл. 5 и 6 приложения.
Параллелепипед со сторонами 
(рис. 4. 2). Безразмерная температура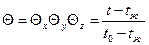 
или
(4. 10)
Рис. 4. 2. Параллелепипед со сторонами 2х, 2у, 2z
Функции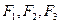 
определяются по формулам (4. 1)–(4. 4), по табл. 5и по графикам рис. П. 1 и П. 2 приложения для бесконечной пластины с учетом места расположения интересующей нас точки в параллелепипеде.
|
|
|
1. 7. 3. Расчет отданной (воспринятой) телом теплоты
Количество теплоты 
, Дж, отданной (воспринятой) телом за время t в процессе охлаждения (нагревания), равно
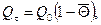(4. 11)
где Qo–количество теплоты, переданной за время полного охлаждения (нагревания), Дж;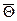 
–средняя по объему безразмерная температура тела в момент времени t.
Для пластины толщиной 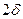и площадью поверхности F теплота. Преданная за время полного охлаждения, равна
(4. 12)
где m–масса пластины, кг; с – удельная теплоемкость материала пластины, Дж/(кг·К); 
–его плотность, кг/м3.
Средняя по объему безразмерная температура пластины в момент времени при Fo> 0, 3 равна
(4. 13)
Для цилиндра радиусом и длиной l теплота, отданная за время полного охлаждения, равна
(4. 14)
Средняя по объему безразмерная температура цилиндра в момент времени при Fo> 0, 3 равна
(4. 15)
Средняя безразмерная температура цилиндра конечной длины
(4. 16)
где функция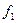 
определяется по формуле (4. 13), а 
– по (4. 15).
Для параллелепипеда со сторонами (рис. 4. 2) теплота, отданная за время полного охлаждения, равна
(4. 17)
Средняя безразмерная температура параллелепипеда
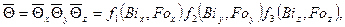(4. 18)
где функции 
определяются по формуле (4. 13).
Если Fo< 0, 3, то для вычисления Q используется ряд, члены которого определяются формулами типа (4. 13), (4. 15), причем величины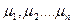 
определяются по таблицам, приведенным, например, [12].
1. 7. 4. Регулярный режим охлаждения (нагревания) тел
Теорию регулярного режима разработал Г. М. Кондратьев. Процесс охлаждения тела в среде с постоянной температурой и постоянным коэффициентом теплоотдачи а можно разделить на три режима
1) неупорядоченный– на процесс влияет начальное распределение температуры в теле;
2) регулярный– в любой точке тела относительная скорость изменения температуры, называемая темпом охлаждения (нагревания) остается постоянной и не зависит от времени;
3) стационарный – температура во всех точках тела равна температуре среды (тепловое равновесие).
В регулярном режиме темп охлаждения (нагревания), т, с-1, определенный по двум моментам времен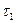и 
и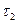 
, равен
(4. 19)
где 
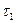–избыточные температуры в любой точке тела в моменты времени и .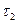
Темп охлаждения m зависит от физических свойств тела, его размеров и формы, коэффициента теплоотдачи и не зависит от времени координат.
|
|
|
Первая теорема Г. М. Кондратьева для регулярного режима. выражается формулой
(4. 20)
где F и V – площадь поверхности и объем тела; 
– коэффициент 1 равномерности распределения температуры в теле, определяемый следующим образом:
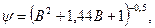(4. 21)
где 
модифицированная форма числа Bi; К–коэффициент формы тела, м2.
Коэффициент зависит от условий процесса на поверхности тел при Bi< 0, l =1 (температуры, усредненные по поверхности и объем тела, одинаковы), при Bi> 100 =0 (температура поверхности тела равна температуре среды).
Вторая теорема Г. М. Кондратьева: при высокой интенсивности теплоотдачи темп охлаждения пропорционален коэффициенту температуропроводности материала тела а,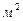 
/с:
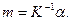(4. 22)
Коэффициент формы К различных тел:
для шара радиусом
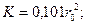(4. 23)
для цилиндра длиной l и радиусом
(4. 24)
для параллелепипеда со сторонами a, b, c
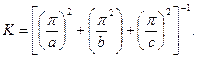(4. 25)
2. Конвективный теплообмен в однородной среде
|
|
|
