1.6.2.2. Граничные условия третьего рода

1. 6. 2. 2. Граничные условия третьего рода

Однородная шаровая стенка. Теплопередача между двумя средами с температурами  и

                           (1. 27)

Коэффициент теплопередачи для однородной стенки, Вт/К,

 

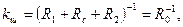                      (1. 28)

где  и -термические сопротивления теплоотдачи; 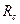– термическое сопротивление теплопроводности стенки; R₀ – общее термическое сопротивление теплопередачи, К/Вт. Т. е.

.

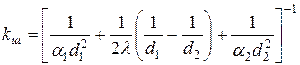Многослойная шаровая стенка. Коэффициент теплопередачи для многослойной стенки, Вт/К,

 

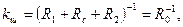                      (1. 28)

где  и -термические сопротивления теплоотдачи; 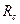– суммарное. термическое сопротивление теплопроводности п слоев стенки; R₀ – общее термическое сопротивление теплопередачи, К/Вт. Т. е.

.

 

1. 6. 3. Теплообмен на ребристой поверхности.

Для интенсификации теплопередачи между двумя, средами применяют оребрение поверхностей стенки, разделяющей эти, среды. Как правило, оребрение осуществляется на той поверхности теплообмена, где имеет место малый коэффициент теплоотдачи (или большое термическое сопротивление).

 

1. 6. 3. 1. Плоская стенка с прямыми ребрами постоянного поперечного сечения                             

Основные параметры ребристой стенки (рис. 2. 1): l, h, –длина высота, толщина ребра; П=2(l+ )–периметр ребра; f=l –площади сечения ребра; b–шаг ребер; В, –ширина и толщина плоской стенки; –температуры сред, окружающих стенку, ,  – коэффициенты теплоотдачи от поверхности ребра и от гладкой поверхности стенки к окружающей среде;  температуры ребра у основания и на его конце.

Рис. 2. 1. Плоская ребристая стен­ка

 

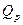При расчете теплоотдачи с поверхности  одного прямого ребра в окружающую среду, имеющую температуру , тепловой поток , Вт, определяется nо формуле

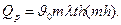                                 (2. 1)

где 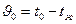–избыточная температура у основания ребра, К;  –параметр. ; th(mh)= 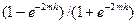 –тангенс гиперболический; – теплопроводность материала ребра Вт/(мК).

Тепловой поток Q_г, Вт, с гладкой поверхности F_г стенки в промежутках между ребрами

                       (2. 2)

где п –количество ребер на 1 м ширины стенки; l – длина стенки (длина ребра), м.                                                  

Суммарный тепловой поток Qo при теплоотдаче с оребренной по­верхности стенки

                               (2. 3)

Тепловой поток, обусловленный теплопередачей между двумя сре­дами, разделенными плоской стенкой, имеющей оребрение с одной сто­роны,

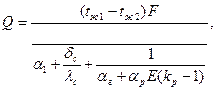                   (2. 4)

где F–площадь неоребренной поверхности стенки, м²; 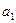–коэффи­циент теплоотдачи на неоребренной поверхности стенки, Вт/( 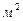К); –теплопроводность материала стенки, Вт/(м·К); Е–коэффициент эффективности ребра; k_p–коэффициент оребрения.

 

Коэффициент эффективности ребра Е является его рабочейхарактеристикой и представляет собой отношение теплового потока, действительно рассеиваемого ребром в окружающую среду, к тепловому потоку который ребро могло бы отдать, если бы вся его поверхность находилась при температуре :

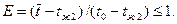                           (2. 5)

или, пренебрегая теплоотдачей с торца ребра,

                         (2. 5a)

где –средняя температура поверхности ребра.

Повышения теплосъема ребра можно добиться при уменьшении mh..

 Коэффициент оребрения

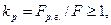                              (2. 6)

где – суммарная площадь оребренной поверхности стенки, м².

В формуле (2. 4) можно положить 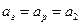, тогда тепловой по­при теплопередаче через оребренную стенку

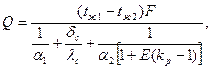                    (2. 7)

а коэффициент эффективности тонкого ребра (в предположении, что 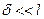 и П==2l) можно определить из зависимости

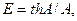                                     (2. 8)

где , или из графика рис. 2. 2.

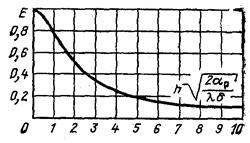
Рис. 2. 2. Коэффициент эффективности Е ребра

 

Для учета теплоотдачи с торцевой поверхности ребра необходимо зысоту ребра h увеличить на 0, 5 .

Температура  на конце ребра

 или 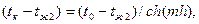(2. 9)

где 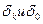 – избыточные температуры на конце ребра и у его осно­вания, К;     ch(mh) =0, 5 ( ) –косинус гиперболический.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: