Магнитный момент изолированного атома

Магнетизм свободного атома имеет 3 главных источника:

-спин электронов,

-их орбитальный момент, и

-изменение в орбитальном моменте, индуцированном внешним магнитным полем.

В рамках классических представлений, магнитный момент, обусловлен классическим орбитальным движением электрона:

 

М _l = n∙ [ток]∙[площадь орбиты] = n∙ [-e| v |/(2πr) ]∙[πr²] = -(1/2)evr n, (1.20)

 

где n – единичный вектор, нормальный к плоскости орбиты, е – заряд электрона, v -скорость его орбитального движения, r – радиус орбиты. В соответствии с классической механикой, P _l = m v×r – орбитальный угловой момент (m – масса покоя электрона). Тогда

М _l = - (e/2m)P_l (в СИ), (1.21а)

М _l = - (e/2mс)P_l (в СГСМ), (1.21б)

соотношение (1.21) показывает, что магнитный момент М _l и орбитальный момент P _l антипараллельны друг другу.

 

Квантовая механика дает то же соотношение, но величина орбитального углового момента дается в единицах постоянной Планка ħ:

P_l = [l(l +1)]^1/2ħ = l ^*ħ, (1.22)

где l – орбитальное квантовое число. Подставляя, (1.22) в (1.21), получаем

М_l = -[μ₀eħ/(2m)]l ^* =

= -μ₀μ_B l ^* в СИ, (1.23а)

М_l = -[eħ/(2mс)]l ^* =

= -μ_Bl ^* в СГСМ, (1.23б)

где магнетон Бора μ_B = eħ/(2m) =

= 9.27∙10^-24А∙м² (СИ), (1.24а)

μ_B = eħ/(2mс) =0.927∙10^-20эрг∙Гс^-1 (СГСМ). (1.24б)

Аналогично (1.22), угловой момент спина

P_s = [s(s+1)]^1/2ħ = s^*ħ, (1.25)

где спиновое квантовое число s = ½, так что s^*=√3/2 всегда.

Но в отличие от (1.23), спиновое гиромагнитное отношение в два раза больше, т.е.

М_s /s^*= -g_sμ_B, где g_s = 2. (1.26)

Если действует спин-орбитальное (или l-s) взаимодействие, (рис. 1.1), то полный угловой момент

P _j = P _l + P _s. (1.27)

Происходит электростатическое взаимодействие между орбитальным движением и спином электрона, поскольку каждое движение производит магнитное поле, влияющее на другое движение. В результате и спин и орбитальный момент прецессируют с одинаковой угловой скоростью, ω, и в одном направлении вокруг общей оси, которой служит результирующий угловой момент

P _j = [j(j+1)]^1/2ħ = j^*ħ, (1.28)

где j = l ± s и j^* = (j(j+1))^1/2.

Однако, как поясняется на рис. 1.1, полный магнитный момент

M _j = M _l + M _s (1.29)

не коллинеарен вектору P _j из-за разницы в g_l = 1 и g_s = 2. Величина M_j будет определяться проекцией M _ls на общую ось прецессии. Тогда,

M_j = - j^*g_jμ_B, (1.30)

g_j = 1 + [(j^*)² - ( l ^*)² + (s^*)²]/2(j^*)² (1.31)

– т.н. фактор Ланде.

 

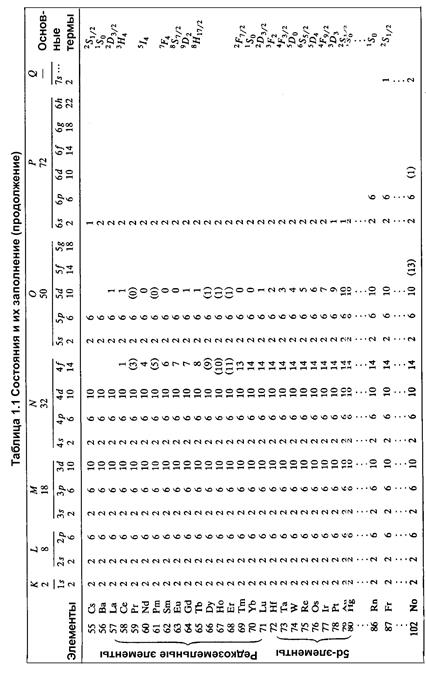
Электронная система атомов состоит из заполненных и незаполненных оболочек. Полный угловой момент, а следовательно, и полный магнитный момент замкнутой оболочки свободного атома равен нулю. Магнитный момент свободного атома, определяется конфигурацией незаполненной электронной оболочки атома. Представление о заполнении электронных оболочек дает таблица 1.1.

Угловые моменты и спины оболочек формируются при электростатическом взаимодействии орбитальных и спиновых моментов электронов оболочки, образующих орбитальный момент оболочки L =Σl_i, (l^*l^*-связь), и электростатическом взаимодействии спиновых моментов электронов оболочки, образующих спиновый момент оболочки S = Σ s _i (s^*s^*-связь). Далее за счет магнитостатической L ^* S ^*-связи, называемой связью Рассела-Саундерса (Russel-Saunders) или LS –связью, формируется полный угловой момент J = L + S. Этот процесс иллюстрируется на рис. 1.2.

Магнитный момент атома в этом случае

M_J = - J^*g_Jμ_B, где J^* = [J(J+1)]^1/2 и (1.32)

 

 

g_J = 1 + [(J^*)² - (L^*)² + (S^*)²]/2(J^*)² – фактор Ланде. (1.33)

 

 

Формирование угловых и спиновых моментов происходит в соответствии с т.н. правилами Хунда.

 

Правила Хунда.

Из всех возможных конфигураций электронов данной оболочки наинизшей энергией будут обладать следующие состояния:

1. С максимальным значением полного спина S, разрешенным принципом Паули.

2. С максимальным значением орбитального углового момента L для данного S (при выполнении 1-го правила)

3. С J = |L - S|, когда оболочка заполнена менее чем на 1/2 и J = L + S, когда оболочка заполнена более чем на 1/2. Когда оболочка заполнена на 1/2 точно, то из 1-го правила следует L = 0, так что J = S.

 

1-ое правило - следствие принципа Паули. Согласно ему электроны с параллельно (­­) –ориентированными спинами будут находиться на более далеком расстоянии, чем электроны с антипараллельно (­¯) - ориентированными спинами, поэтому кулоновская энергия отталкивания (­­)-электронов будет меньше.

Пример: Mn²⁺ - имеет конфигурацию [Ar]3d⁵ (4s² -внешние электроны удалены). 5 электронов на d-оболочке, заполняют ее на 1/2. Спины могут быть ­­-ными, если все электроны будут на разных орбиталях с m_L = 2, 1, 0, -1, -2. Спин будет равен S=5/2, Sm_L = 0 и соответственно, L = 0, что и наблюдается экспериментально.

2-ое правило - подтверждается экспериментально. 3-ье правило Хунда определяется знаком спин-орбитального взаимодействия, которое снимает (2L+1)(2S+1)- вырождение и в гамильтониане может быть описано членом

l (L×S). (1.34)

Для одиноких на орбите электронов l>0. Для оболочек, заполненных более чем на половину, l<0. За счет спин-орбитального взаимодействия при l<0 выгодно состояние с максимальным значением J (орбитальный момент параллелен спиновому), при l>0 выгодно состояние с минимальным значением J (орбитальный момент антипараллелен спиновому).

Пример: а) Ce³⁺(церий) (Ce=[Xe]4f¹5d¹6s²®Ce³⁺ [Xe]4f¹) имеет 1 электрон на f-оболочке, L = 3, S =1/2. Поскольку f-оболочка заполнена менее чем на 1/2, значение J = |L-S| = 3-1/2 = 5/2.

б) Pr³⁺[празеодим]{Pr=[Xe]4f³5d⁰6s²]®[Xe]4f²}. По 1-му правилу S = 1, по 2-му - L = 3+2=5. J = |L-S| = 5-1 = 4.

 

Правила Хунда иллюстрируются таблицей 1.2 на примере заполнения d-оболочки и рис. 1.3 на примере 4f-элементов

 

Таблица 1.2. Схема формирования основных состояний ионов с частично заполненной d-оболочкой, в соответствии с правилами Хунда.

 

Магнитные моменты атомов и молекул во внешнем магнитном поле.

Эффект расщепления энергетических уровней в магнитном поле (эффект Зеемана) наблюдается, когда поле достаточно слабо и не разрушает LS -связь, рис. 1.4. В противном случае, орбитальный и спиновый угловые (и магнитные) моменты прецессируют независимо вокруг направления поля (эффект Пашена-Бэка), что приводит к разрыву LS -связи.

 

Гамильтониан взаимодействия атомов и молекул с магнитным полем, расщепление уровней.

В однородном магнитном поле гамильтониан изменяется следующим образом:

1. Импульс p _i® p _i + (e/c)· A (r _i). (1.35)

Векторный потенциал выбираем в виде A = -1/2 [ r H ], (1.36а)

так что rot A º[ Ñ * A ]= H и div A º ÑA =0. (1.36б)

2. В гамильтониан H должна быть включена энергия взаимодействия поля со спином

D H = g₀m_B НS_Z (где S_Z=å_i s_zⁱ). (1.37)

Магнетон Бора m_B=eh/2mc =0.927*10^-20эрг/гс=0.579*10^-8эв/гс, а g₀ – спиновый электронный g-фактор

g₀=2[1+a/2p +О(a²)+....] = 2.0023; a = e²/hc» 1/137

обычно полагают g₀ » 2.

 

В соответствии с (1.20) оператор кинетической энергии

T=1/2m å_i[ p _i+e/c A (r _i)]²=1/2m å_i(p _i-e/2c [ r _i* H ])². (1.38)

Соотношение (1.24) можно представить в виде

T=T₀+m_B LH +(e²/8mc²)H²å_i(x_i²+y_i²), (1.39)

где T₀-немагнитная составляющая, L - суммарный орбитальный момент электронов

h L =å_i[ r _i* p_i ]. (1.40)

Объединяя (1.25) и (1.23), получаем, что зависимость от поля определяется следующими членами в гамильтониане:

D H =m_B(L +g₀ S) H +(e²/8mc²)H²å_i(x_i²+y_i²). (1.41)

Изменение энергии (1.27) оказывается малым по сравнению с энергией атомных возбуждений, поэтому применима теория возмущений. Поскольку восприимчивость c ~ ¶²U/¶H², то необходимо учесть члены до 2-го порядка по H включительно

E_n®E_n+DE_n;

DE_n=<nêD H ên>+å_{n'¹ n} {ê<nêD H ên'>ê² / (E_n-E_n')}. (1.42)

DEn=mBH<nêL+g­0Sên> + ån'¹n{ê<nêmBH(L+g0S)ên'>ê2/(En-En')} +(e2/8mc2) H2<nêåi(xi2+yi2)ên>. (1.43)

Подставляя (1.41) в (1.42) и учитывая только линейные и квадратичные члены по H, получаем

 

Выражение (1.43) лежит в основе теоретического описания восприимчивости отдельных атомов, ионов и молекул. На нем базируется также теория восприимчивости ионных и молекулярных кристаллов, т.е. тех твердых тел, которые могут быть представлены как совокупность слабо деформированных свободных ионов. В этих случаях восприимчивость вычисляется посредством суммирования вкладов отдельных ионов.

Линейный по Н член в (1.43) почти всегда будет доминировать, даже при очень сильных полях (~ 10⁴ Гc), если, конечно, он не обращается в 0. В этом случае <nêL_z+g₀S_Zên>~ 1 и тогда

m_B H <nê L +g­₀ S ên> = O(m_BH) ~ heH/2mc ~ hw_c, (1.44)

где w_c = eH/2mc (CГС) [w_с =eH/2m (СИ)] – т.н. циклотронная частота.

При H~10⁴ Гс эта величина ~10^-4 эв, что, в соответствии с ранее сказанным о малости магнитных сдвигов, значительно ниже тепловой энергии (при комнатной температуре - 25 мэВ) и, тем более, энергии возбуждения атомных уровней и энергий межзонных переходов (>~ эВ).

В третьем члене в (1.29) <nêå_i(x_i²+y_i²)ên> имеет порядок квадрата типичного атомного размера, поэтому

(e²/8mc²)H²<nêå_i(x_i²+y_i²)ên>=O[(eH/2mc)²ma₀²]» hw_c(hw_c/(e²/a₀)), (1.45)

где a₀= h²/me² = 0.529 10^-8 cм - боровский радиус.

Поскольку e²/a₀ » 27эв, то (1.31) меньше (1.30) в ~ 10⁵ раз, даже в сильных полях ~ 10⁴ Гc.

Можно показать, что второй член в (1.43) å_n'¹n{ê<nêm_B H (L +g₀ S)ên'>ê²/(E_n-E_n')} также меньше 1-го m_B H <nê L +g­₀ S ên>. Их отношение - величина порядка hw_c/D, где D=minêE_n-E_n'ê- типичная энергия атомного возбуждения. В большинстве случаев D достаточно велика, чтобы отношение hw_c/D можно было считать весьма малым.

II. ДИАМАГНЕТИЗМ

Ларморовский диамагнетизм атомов с полностью заполненными внутренними оболочками

У ионов с полностью заполненными оболочками (например, F^-..., Li⁺...) ® спин и орбитальный момент = 0. Поэтому, в основном состоянии ê0>: J ê0> = L ê0> = S ê0> = 0. Следовательно, изменение энергии основного состояния под действием поля возникает только за счет 3-го члена в (1.43).

DE₀ = (e²/(8mc²)) H ² <0êå_i(x_i²+y_i²)ê0> = e² H ²/(12mc²) <0êå_ir_i²ê0>. (2.1)

Если при термодинамическом равновесии вероятность обнаружить ион в каком-либо состоянии, отличном от основного, пренебрежимо мала (это условие выполняется практически при всех не очень высоких температурах), то восприимчивость твердого тела, состоящего из N-ионов, определяется выражением

c = -N/V ¶²DE₀/¶H²= -e²/(6mc²) N/V <0êå_ir_i²ê0>. (2.2)

Это формула Ланжевена (P. Langevin, 1905) для т.н. ларморовского диамагнетизма. Величины c для некоторых атомов инертных газов и ионов щелочно-галлоидных соединений (ЩГС) приведены в таблицу 2.1.

 

 

Таблица 2.1 Молярные восприимчивости (в единицах 10^-6 см³/моль) атомов и ионов ЩГС.

He - 1.9	Li+ -0.7	F- - 9.4
Ne - 7.2	Na+ -6.1	Cl - -24.2
Ar - 19.4	K+ -14.6	Br-- -34.5
Kr - 28.	Rb+ -22.0	I- -50.6
Xe - 43.	Cs+ -35.1

 

 

Диамагнетизм является универсальным свойством, присущим всем веществам. Ларморовский диамагнетизм ассоциируется со стремлением электрических зарядов экранировать внутренний объем тела от воздействия прилагаемого магнитного поля, аналогично закону Ленца (наведенный ток препятствует изменению электрического потока через контур).

В создании диамагнитного момента участвуют все электроны атома, а также свободные носители. Поэтому, матричный элемент в (2.2) нормируют на полное число электронов

<r²> = <0êå_ir_i²ê0> / Z _i, (2.3)

а c приводят, как в таблице 2.1, в молекулярных единицах.

Таким образом,

c^mol = -Z _iN_A e²/(6mc²) <r²>= -0.79Z_i 10^-6<(r/a₀)²> см³/моль, (2.4)

Отсюда следует, что c^mol ~ 10^-5, т.е. I<<H, в соответствии с приводимыми ранее оценками и таблице 2.1.

На квазиклассическом языке диамагнетизм атомов и молекул описывают, используя теорему Лармора (Larmor):

в магнитном поле движение электронов вокруг ядра, в первом приближении по Н, то же что и без магнитного поля, за исключением прецессии электронов с угловой (ларморовской или циклотронной) частотой w_с.

Если средний ток электронов вокруг ядра исходно = 0, то при включении Н возникает конечный ток вокруг ядра. Ток порождает магнитный момент, направленный против прикладываемого поля. Предполагается, что ларморовская частота << частоты исходного движения в центральном поле ядра. Ларморовская прецессия Z электронов эквивалентна току

i = (заряд)*(число оборотов в ед.времени) =

= (-Ze)(1/2p)(eН/2mc)(CГС). (2.5)

Магнитный момент M = (ток)*(площадь контура). Если радиус контура = r, то

M = -Ze²H/4mc² <r²> (CГС);

M = -Ze²H/4m <r²> (СИ). (2.6)

Поскольку величина <r²>=<x²>+<y²> = 2/3 (<x²>+<y²>+<z²>) = 2/3 <r²> и тогда диамагнитная восприимчивость единицы объема:

c=NM/H = -(NZe²/6mc²) <r²> (CGS);

c= -m₀NM/H= - (m₀NZe²/6m) <r²> (СИ). (2.7)

что совпадает с (2.4).

 

 

III. ПАРАМАГНЕТИЗМ

 

 

Парамагнетизм (c>0,c~10^-5 - 10^-2) обнаруживается:

1. В атомах, молекулах и в дефектах решетки, обладающих нечетным числом электронов, и, следовательно, ненулевым полным спином. Примеры: свободные атомы Na, газообразный NO, F-центры в щелочно-галлоидных соединениях (ЩГС).

2. В свободных атомах и ионах с частично заполненными внутренними оболочками: переходных элементах; ионах, изоэлектронных с переходными элементами; редкоземельных атомах и актиноидах. Примеры: Mn²⁺,Gd³⁺,U⁴⁺. Парамагнетизм проявляется во многих из этих атомов, даже в том случае, когда они внедрены в решетку, но величина восприимчивости при этом изменяется.

3. В некоторых соединениях с четным числом электронов, включая молекулярный кислород и органические бирадикалы, когда имеется нескомпенсированный спин электронов.

4. В ферромагнетиках при Т>Т_К^.

5. Во многих других металлах.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: