Ланжевеновский парамагнетизм

Функция Ланжевена.

Иначе говоря, парамагнетизм наблюдается в веществах, где атомы, ионы, молекулы или дефекты имеют нескомпенсированный угловой и, следовательно, магнитный моменты, что и отличает их от диамагнетиков. При этом магнитные моменты разнесены в пространстве настолько, что они не взаимодействуют друг с другом.

Рассмотрим систему N магнитных атомов, каждый из которых имеет магнитный момент М (Вб м в СИ). Если М=1m_В, то в поле Н = 1МА/м (»12 кЭ) атом имеет дополнительную энергию МН»1.2·10^-29·10⁶ = 1.2·10^-23Дж. В то время как тепловая энергия при комнатной температуре ½ kT =1/2·1.38·10^-23·300 = 2.1·10^-21Дж, т.е. в 175 раз выше. Очевидно, что тепловые колебания сильно влияют на пространственное распределение моментов, определяя тенденцию к однородному распределению. Точнее, распределение в классическом описании будет больцмановским: exp(-U/kT) = exp (MHcosq/kT). Представляя распределение в виде распределения по сфере, вероятность магнитному моменту быть в угловом диапазоне q - (q+dq):

. (3.1)

Полная намагниченность будет определяться средним значением косинуса угла q:

(3.2)

Полагая МН/kT = a, cosq=x, интегрируем (3.2) и получаем

(3.3)

где L(a)­= [ctha-1/a] (3.4)

– функция Ланжевена. С ростом a L(a) стремится к единице (рис.3.1), а, следовательно, с ростом Н I à NM, что соответствует полному выстраиванию магнитных моментов. Однако этот предел не достижим без супервысоких полей, поскольку в нормальных (хоть и высоких) полях Н ~1МА/м a = MH/(kT) ~ 1.2·10^-23/4.2·10^-21~0.003. При столь малых величинах аргумента I (α) практически линейна.

 

Закон Кюри.

При малых α функция Ланжевена разлагается в ряд

L (α) = α/3 – α³/45 + … (3.5)

Оставляя только линейный член в (3.5), имеем

I = NMα /3 = NM ² H /(3kT). (3.6а)

Соответственно, для восприимчивости

c = I/H = NM ²/3kT - закон Кюри. (3.6б)

 

 

Функция Бриллюэна.

В квантовомеханическом описании магнитный момент занимает дискретные положения. Если сориентировать ось z вдоль внешнего поля, то z -компонента поля магнитного момента, то

M_z = g m _BJ_z, (3.7)

где J_z принимает 2J +1 значение от – J до + J. В этом случае средняя намагниченность в магнитном поле имеет вид

 

, (3.8)

 

где α=Jgm_BH/kT, а выражение в квадратных скобках 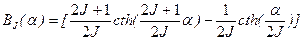(3.9)

называется функцией Бриллюэна. На рис.3.2 показаны кривые намагниченности для парамагнитных солей, содержащих ионы Cr³⁺, Fe³⁺ и Gd³⁺ [W.E. Henry, Phys. Rev., 88 (1952), 552]. При J à∞ функции Бриллюэна и Ланжевена совпадают. При α<<1

(3.10)

Полагая J à∞ в (3.10) мы находим, что (3.10) совпадает с (3.5). Таким образом, функция Бриллюэна включает функцию Ланжевена как специальный случай (J à∞). Учитывая, что α = Jg m _BH/kT и ограничиваясь первым членом в (3.10), мы получаем тот же закон Кюри, называемый еще законом Кюри-Бриллюэна:

c = Ng²J(J+1) m _B ²/3kT. (3.11)

Видно, что (3.11) совпадает с (3.6), если

M_eff = g [J(J+1)]^1/2m _B. (3.12)

M_eff называют эффективным магнитным моментом.

Рассмотрим проявление парамагнетизма в конкретных случаях.

В случае J¹0 первый член в (1.43) m_B H <nï L+g₀S ïn> не обращается в нуль и имеет вклад настолько большой, что всеми остальными можно пренебречь. Справедливо описание, изложенное выше при выводе функции Бриллюэна.

Магнитный момент атома дается соотношением (1.32) M_J = - J*g_Jμ_B, где - векторная сумма L* и S*. Т.е. магнитный момент, в принципе, определяется как орбитальным, так и спиновым моментом. Однако, как следует из последующего, в ряде случаев L* = 0, тогда J* = S* и g_J = g_S =2. Т.е. когда М = М_S =2S*m_B, это говорит о том, что магнитный момент полностью обусловлен спином. В этом случае говорят, что орбитальное движение, орбитальный угловой момент и орбитальный магнитный момент «заморожены» (quenched).

Эффект замораживания углового момента наблюдается в большинстве переходных металлических ионов и атомов, но редко в лантаноидах. Экспериментальные доказательства эффекта получают из данных по магнитной восприимчивости.

 

Парамагнетизм редкоземельных ионов.

Закон Кюри c~1/T хорошо выполняется для редкоземельных (РЗ) ионов, содержащих частично заполненные оболочки, в диэлектрических кристаллах. РЗ-ионы имеют очень похожие химические свойства. Ионы имеют валентность = 3 и их внешние оболочки имеют конфигурацию 5s²5p⁶ как и нейтральный Xe. В предшествующем La 4f-оболочки не заполнены, а в Ce³⁺- 4f¹ и далее число 4f-электронов возрастает непрерывно в группе, достигая 4f¹³ в иттербии,Yb³⁺ и заполняя оболочку в Lu³⁺®4f¹⁴. Радиусы 3+ ионов плавно варьируются от 1.11A⁰(Ce³⁺) до 0.94 A⁰(Yb³⁺) - "сжатие лантаноидов". Число электронов на внутренней 4f-оболочке с радиусом»0.3А отличает один лантаноид от другого. В металлическом состоянии 4f электроны сохраняют свою конфигурацию и атомные свойства. (2J+1)-кратное вырождение снимается в магнитном поле.

Согласно закону Кюри-Бриллюэна (3.11) при

gJ*m_BH/k_BT<<1 ® c=M/H= N/V p²m_B²/3k_BT, (3.13)

где p=g[J(J+1)]^1/2 - (3.14)

эффективное число магнетонов Бора. Для многих РЗ теоретические значения р согласуются с экспериментальными:

Ce³⁺ 4f¹5s²p^{6 2}F(L=3)_5/2 p(теор) = 2.54 р(эксп)=2.4

Pr³⁺ 4f²5s²p^{6 3}H(L=4)₄ р(теор) = 3.58 р(эксп)=3.5

Однако для некоторых других РЗ наблюдается достаточно большое расхождение:

Sm³⁺ 4f⁵5s²p⁶ 6H_5/2 р(теор)=0.84 р(эксп) =1.5

Eu³⁺ 4f⁶5s²p⁶ 7F₀ р(теор)=0 р(эксп) =3.4

Расхождение показывает, что необходимо учитывать влияние более высоких уровней L-S мультиплета, поскольку расстояние между мультиплетными уровнями оказывается не очень большим по сравнению с k_BT при комнатной температуре. В результате при данных L и S возбуждаются состояния с различными J, которые перемешиваются.

 

Парамагнетизм переходных элементов группы железа.

Как показывает сопоставление теоретических магнитных моментов (чисел магнетонов р)

M@pm_B p=g[J(J+1)]^1/2 (3.15)

и экспериментальных р(эксп), имеется большое расхождение между ними. Расчетные значения эффективных чисел магнетонов приведены в таблице 3.3 для двух альтернативных предположений, согласно первому из них эффективное число магнетонов определяется полным угловым моментом, р(J)=g[J(J+1)]^1/2, по второму - р(S)=2[S(S+1)]^1/2.

 

Таблица 3.3. Эффективное число магнетонов для некоторых 3d-ионов.

Ионы Конфигурация р(J) р(S) p(экс)

Ti³⁺,V⁴⁺ 3d^{1 2}D_3/2 1.55 1.73 1.8

V³⁺ 3d^{2 3}F₃² 1.63 2.83 2.8

Cr³⁺,V²⁺, Mn⁴⁺ 3d^{3 4}F_3/2³ 0.77 3.87 3.7, 3.8, 4.0

Cr²⁺, Mn³⁺ 3d^{4 5}D₀ 4.90 0 4.8, 5.0

Fe³⁺, Mn²⁺ 3d^{5 6}F_5/2 5.92 5.92 5.9

Fe²⁺ 3d^{6 5}D₄ 6.70 4.90 5.4

Co²⁺ 3d^{7 4}F_9/2 6.63 3.87 4.8

Ni^{2+ 3}F₄ 5.59 2.83 3.2

Cu²⁺ 3d^{9 2}D_5/2 3.55 1.73 1.9

 

Можно заметить из сравнения, что экспериментальные значения во многих случаях ближе к р(S)=2[S(S+1)]^1/2, так как будто бы орбитальные моменты не участвуют в формировании магнитного момента. Это и есть уже упомянутый эффект замораживания орбитального углового момента.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: