 |
Связь между частотными критериями устойчивости и методами выделения области устойчивости в пространстве параметров.
|
|
|
|
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
Методы математического описания линейных систем управления.
1) Линейные дифференциальные уравнения
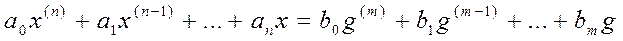
Здесь 
- постоянные коэффициенты, x - выходная величина динамической системы, g - входная величина. Дифференциальное уравнение полностью описывает свойства линейной динамической системы (не обязательно системы управления).
2) При исследовании свойств систем управления в ряде случаев более удобным представляется частотный оператор, который также служит полной характеристикой линейной динамической системы. Для получения выражения частотного оператора подадим на вход линейной системы входное тестовое гармоническое
и попробуем найти выходную величину в форме
Дифференцируя по времени t получаем выражение для частотного оператора
.
Частотный оператор линейной динамической системы представляет дробно-рациональную функцию величины 
, 
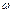- частота входного тестового гармонического воздействия. Сам оператор является комплексной функцией и может быть записан в форме
;
здесь 
- модуль частотного оператора и называется амплитудной частотной характеристикой, 
- аргумент частотного оператора и называется фазовой частотной характеристикой. Нетрудно выяснить тот факт, что амплитудная частотная характеристика является четной, а фазовая частотная характеристика - нечетной функцией частоты.
Из физических наблюдений известно, что с увеличением частоты входного воздействия амплитуда на выходе убывает (по крайней мере, начиная с некоторого значения частоты). Это объясняется тем, что порядок знаменателя, вообще говоря, выше порядка числителя. Это свойство частотного оператора называют свойством физической осуществимости
|
|
|
3) Среди тестовых сигналов особая роль принадлежит δфункции или функции Дирака. Реакция динамической системы на это входное воздействие называется импульсной переходной характеристикой, которую обычно обозначают символом 
. Пользуясь этим понятием, можно получить выражение для вычисления реакции системы на воздействие произвольного типа, в том числе и на воздействие типа непрерывной функции времени.
Формально импульсную переходную характеристику можно определить как оригинал по отношению к передаточной функции.
.
Связь между частотными критериями устойчивости и методами выделения области устойчивости в пространстве параметров.
Итак, пусть передаточная функция разомкнутой системы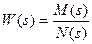 
.
Тогда характеристическое уравнение замкнутой системы 
, (9.5)
и мы рассмотрим однопараметрическое семейство уравнений 
,(9.6) которое при w =1 переходит в (9.5)
Поставим задачу выделения области устойчивости в плоскости параметра w. В соответствии с разработанной методикой заменим
на 
и разрешим (9.6) относительно параметра 
. 
.
Как видим, получилось выражение, совпадающее с точностью до знака с частотным оператором разомкнутой системы. Построение годографа, повернутого на 180о, полностью решает задачу выделения области устойчивости (рис.9.6)
Рис.9.6.Годограф Найквиста как граница области устойчивости
Если действительная единица принадлежит области устойчивости, то характеристическое уравнение (9.5) имеет все корни с отрицательной действительной частью. Это утверждение находится в полном соответствии с критерием Найквиста, который сформулирован в лекции 8.
С небольшими изменениями можно установить связь метода выделения области устойчивости с частотным критерием Михайлова. Для этого следует рассмотреть однопараметрическое семейство характеристических уравнений 
,
|
|
|
и построить годограф Михайлова (рис.9.7). При 
мы получаем характеристическое уравнение замкнутой системы и если эта точка принадлежит области устойчивости, то все корни имеют отрицательные действительные части. Это имеет место лишь в том случае, если годограф монотонно проходит 2 n квадрантов (диапазон изменения частоты увеличен вдвое).
Рис.9.7.Годограф Михайлова как граница области устойчивости.
Приведенные здесь примеры выделения областей устойчивости использовали в большой степени аналитический аппарат, позволяющий обходиться без решения алгебраического уравнения порядка выше второго. Современное математическое обеспечение существенно расширило возможности определения областей устойчивости, что особенно ценно при синтезе автоматических систем.
|
|
|
