 |
Оптимальный переходный процесс. Возможности реализации.
|
|
|
|
Пусть на вход системы подается управляющее воздействие типа скачка определенной величины. Требуется отработать этот скачок за минимально возможное время. При этом имеются в виду ограничения, накладываемые характеристиками исполнительного элемента. В случае следящей системы, осуществляющей поворот на заданный угол, таким ограничением служит предельный крутящий момент, который может развить двигатель. Если величина скачка равна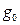 
, то наиболее быстрый поворот на этот угол произойдет, если двигатель его первую половину будет вращаться с максимальным ускорением, а вторую – с максимально допустимым торможением. На рис.11.1 изображен график такого переходного процесса, который мы назовем оптимальным.
Этот принцип осуществления оптимального переходного процесса находится в противоречии с допущением о линейности следящей системы, ибо в линейной системе не предполагается ограничений по какой-либо переменной. При попытке осуществить этот процесс в рамках линейной теории, мы неизбежно обнаружим его неосуществимость. Тем не менее, полезно иметь в виду некоторую идеальную характеристику, которую следует реализовать со всем возможным приближением.
С этой целью найдем изображение оптимального переходного процесса по Лапласу. Затем, составив отношение полученного изображения к изображению скачка, попытаемся получить оптимальную передаточную функцию.
Итак, разгон двигателя происходит по закону 
,
где а – предельное угловое ускорение, которое можно найти из очевидного соотношения 
.
Далее, оптимальный переходный процесс можно представить в виде суммы
.
Преобразуя по Лапласу, имеем 
.
Изображение входного скачка 
.
|
|
|
и, следовательно, искомая передаточная функция замкнутой следящей системы
. (11.1)
Полученное выражение показывает, что оптимальная передаточная функция не может быть реализована линейными средствами, ибо передаточные функции линейных систем принадлежат к классу дробно-рациональных функций переменной s, в то время как в (11.1) мы имеем набор трансцендентных функций, не принадлежащих к классу полиномов.
Построим передаточную функцию разомкнутой системы, используя очевидное соотношение
. (11.2)
Прежде всего, интересно асимптотическое поведение этой функции при 
. Для выяснения этого достаточно выписать разложение числителя в окрестности нуля до четвертого порядка:
.
Нетрудно заметить, что в знаменателе (11.2) ряд начнется с третьей степени параметра s, в то время как в числителе нет степени ниже второй. Следовательно, асимптотическое поведение передаточной функции определяется величиной 1/ s, т.е. наклон низкочастотной асимптоты составляет –20 дБ/дек как у системы первого порядка астатизма.
Далее, следует выяснить, какова частота среза амплитудной частотной характеристики 
. Значение этой частоты находится из условия 
, (11.3)
т.е. на этой частоте логарифмическая амплитудная характеристика разомкнутой системы пересекает линию нулевых децибел. Для вычисления этой частоты заметим, что ввиду (11.3) можно записать 
, где 
- некоторый фазовый угол, соответствующий частоте среза.
Имея в виду связь между передаточными функциями разомкнутой и замкнутой систем, запишем также 
.
Таким образом, на частоте среза всегда действительная частотная характеристика замкнутой системы равна 0.5. Воспользовавшись полученным результатом, выделим действительную часть из (11.1). Обозначив для краткости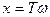 
,
получаем уравнение относительно x 
. (11.4)
На рис.11.2 показан график левой части, из которого видно, что помимо корня x= 0, это уравнение имеет еще два корня, весьма близких к 2 по абсолютной величине. Ограничиваясь положитель-
|
|
|
Рис.11.2.Графическое решение уравнения (11.4).
ным корнем, приходим к заключению о величине частоты среза оптимальной частотной характеристики разомкнутой системы 
.
Графическое изображение этой характеристики дает полное представление о свойствах оптимальной передаточной функции. На рис.11.3 виден, в частности весьма сложный характер ее поведения в области высоких частот, что заставляет еще раз убедиться в неосуществимости реализации оптимального переходного процесса в линейных системах с сосредоточенными параметрами. Однако этот же график в области средних и низких частот вполне реализуется обычными линейными средствами. К этому следует добавить, что очень часто форма частотной характеристики в высокочастотной области не оказывает заметного влияния на форму переходного процесса. Поэтому полученные результаты оказываются полезными при конструировании следящих систем на стадии предварительного синтеза.
Рис.11.3.Логарифмическая амплитудная частотная характеристика оптимальной разомкнутой системы.
|
|
|
