 |
Вынужденные колебания в нелинейных системах. Пороговая амплитуда возбуждающего сигнала. Вибрационное сглаживание разрывных характеристик.
|
|
|
|
Исследование вынужденных колебаний в нелинейных системах связано с определенными затруднениями из-за невозможности применения принципа суперпозиции, которым мы часто пользовались при исследовании линейных систем. Если на вход нелинейной системы поступает гармоническое воздействие, то на ее выходе возникает сложный многочастотный режим. Принцип гармонической линеаризации основан на отбрасывании высших гармоник. При этом рассматриваются наиболее простые одночастотные вынужденные колебания. На рис.26.1 представлена структурная схема с периодическим воздействием на входе.
Рис.26.1. Система с периодическим воздействием на входе.
Применяя принцип гармонической линеаризации, запишем нелинейную характеристику в виде 
.
Предполагая, что выход нелинейной системы - гармоническая функция той же частоты, что и входное воздействие, запишем 
.
Заменив, как обычно, в операторах, показанных на структурной схеме s на j, имеем 
.
Т.к. экспоненциальная функция не обращается в нуль ни при каком значении времени t, то в результате сокращения получаем
(26.1)
Уравнение (26.1) содержит две неизвестные величины: амплитуду a установившихся колебаний выходной координаты и ее фазу . Решение уравнения можно получить, имея в виду весьма прозрачное графическое толкование. Записав уравнение в форме
, (26.2)
замечаем, что правая часть не зависит от частоты и при изменении фазы в пределах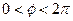 
геометрически соответствует окружности радиуса B. Левая же часть Z(a,) при фиксированном значении амплитуды a и переменной частоте соответствует некоторому годографу, который может быть построен по обычным правилам (с выделением вещественной и мнимой частей). На рис.26.2 показаны годограф левой части уравнения (26.1) и окружность радиуса B с центром в начале координат.
|
|
|
Рис.26.2.Графическое решение уравнения (26.2)
Из рис.26.2 видно, что при значении амплитуды внешнего воздействия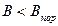 
решения уравнения (26.2) не существует. При радиусе окружности, превышающем пороговое значения амплитуды внешнего воздействия решение возможно в точке пересечения годографа левой части Z(a, ) с окружностью. При этом определяется значение частоты и фазы при выбранном значении амплитуды a для построения годографа. Можно поступить наоборот – построить семейство годографов с параметром a и набора фиксированных значений частоты и определить пороговую амплитуду входного воздействия, при которой одночастотный режим возникает на выходе нелинейной системы. При этом можно выявить резонансные свойства системы, а также явление так называемого захвата частоты. Таким путем можно получить зависимость порогового значения входного воздействия от частоты (рис.26.3). С другой стороны можно получить однопараметрическое семейство частотных характеристик нелинейной системы, т.е. зависимости амплитуды выходного сигнала от частоты для различных значений амплитуды входного воздействия. Здесь следует вспомнить, что в случае линейной системы амплитудная частотная характеристика не зависела от амплитуды входного воздействия.
Рис.26.3. Зависимость пороговой амплитуды
от частоты возмущающего воздействия
На рис.26.3 изображена зависимость, характерная для нелинейной системы с выраженными резонансными свойствами. У нее существует некоторый отличный от нуля интервал частот, на которых происходит навязывание частоты внешнего воздействия даже при очень малых значениях амплитуды. Вне этого интервала при недостаточно большой амплитуде возникают лишь многочастотные режимы, математическая модель которых выходит за рамки основной гипотезы, принятой нами в самом начале относительно вида выходного сигнала. Исследование этих режимов требует более подробного математического моделирования.
|
|
|
Особенно интересным представляется случай, когда на вход нелинейной системы поступают два входных воздействия – «медленное» g (t) и «быстрое» f (t). Дополним уравнение (26.1) и запишем соответствующее соотношение в виде 
. (26.3)
Здесь быстрое воздействие по-прежнему будем считать гармоническим, т.е., например,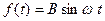 
.
Медленное же воздействие (например, управляющее) таково, что его изменением можно пренебречь на протяжении одного периода 2 быстрых колебаний. Решение уравнения (26.3) на этот раз будем искать в виде 
,где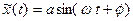 
- периодическая часть решения, а 
- медленная часть реакции нелинейной системы на сумму быстрого и медленного входных воздействий. Соответственно при гармонической линеаризации нелинейную характеристику представим в виде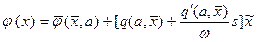 
.
Здесь коэффициенты гармонической линеаризации вычисляются по формулам
, 
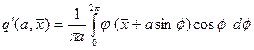, (26.4)
.
Вставим выражения (26.4) вместо 
в уравнение (26.3 и выделим быструю и медленную часть из полученного результата.
, 
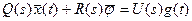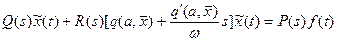(26.5)
Систему (26.5) следует решить относительно a и 
, затем, сопоставив эти решения, получить вместо функции двух переменных зависимость 
.
Любопытно, что последняя зависимость является непрерывной функцией переменной даже в случае разрывной нелинейной характеристики Мы продемонстрируем этот факт на простом примере. Возникновение гладкой функции 
в присутствии высокочастотного гармонического сигнала принято называть вибрационным сглаживанием.
Пример 26.1.
Пусть 
и найдем 
.
Необходимые вычисления выполняются достаточно просто, если воспользоваться графиком подынтегральной функции (рис.26.4), которая в данном случае является кусочно-постоянной. Таким образом, 
.
Здесь угол 
находится из очевидного равенства 
,
Откуда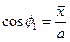 
.
Рис.26.4. Вибрационное сглаживание в случае
разрывной характеристики.
Следовательно, 
.
Линеаризация этой характеристики выполняется обычным путем, т.е. построением касательной в точке 
. Окончательно имеем 
.
Полученный результат можно теперь подставить в «медленное» уравнение (первое уравнение (26.5)) и в дальнейшем исследовать его методами линейной теории. Итак, процесс управления при наличии вибраций описывается уравнением 
.
|
|
|
Возникновение гладкой функции в присутствии высокочастотного гармонического сигнала принято называть вибрационным сглаживанием.
|
|
|
