 |
Знакоопределенные и знакопостоянные функции. Связь с устойчивостью нелинейных систем.
|
|
|
|
Рассмотрим функцию 
на некотором множестве 
.
Здесь 
- n -мерный вектор. Действительная непрерывная функция 
называется знакопостоянной (знакоположительной или знакоотрицательной), если 
(или 
) при 
.
Далее, функция 
называется положительно определенной,в Z, если существует скалярная функция 
, такая, что
при 
,
.
Пример 28.1.
Функция 
при 
является положительно определенной, т.к.
при x 2 + y 2 > 0; V = W= 0 при x = y = 0.
При 
функция V всего лишь знакоположительна.
Аналогично функция V (t, X) называется отрицательно определенной в Z, если найдется 
такая, что
при
и .
Положительно или отрицательно определенная функция называется знакоопределенной.
В теории автоматического управления функции, обладающие свойством положительной (или отрицательной) определенности введены А.М. Ляпуновым и играют основную роль при анализе устойчивости. Они могут принадлежать к различным классам. Нас, в частности, будут интересовать квадратичные формы, т.е. скалярные произведения вида 
, где A=A T – симметрическая матрица порядка 
, а X= (x 1, x 2 ,…, x n)T – вектор-столбец того же порядка. Таким образом, скалярная квадратичная форма записывается в виде
.(28.1)
Матрица A называется матрицей квадратичной формы. Очевидно, матрица и функция (28.1) связаны взимнооднозначно.
Для выяснения свойства положительной определенности функции (28.1) служит критерий Сильвестра:
Для того, чтобы квадратичная форма V (X) была положительно определенной, необходимо и достаточно, чтобы определитель матрицы A и все ее диагональные миноры были положительны.
Пример 28.2.
Форма
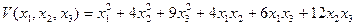
не является положительно определенной. В самом деле, определитель
.
Заметим, что нулю равен и диагональный минор второго порядка.
|
|
|
Нетрудно убедиться, что форма 
положительно определенная.
Вернемся теперь к понятию устойчивости движения, с которым мы познакомились в прошлом семестре (см. лекцию 7) и введем некоторые дополнительные определения.
Пусть снова 
,(28.2)
где 
- вектор состояния системы. При фиксированных компонентах вектор состояния, как мы знаем, указывает точку фазового пространства. Невозмущенным движением называется ограниченный вектор 
, удовлетворяющий уравнению (28.2), т.е. 
.(28.3)
Разность 
называется возмущением. Вычитая (28.3) из (28.2), получаем дифференциальное уравнение в терминах возмущения
, (28.4)
которое, очевидно, обладает тривиальным решением 
.В пространстве 
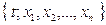это тривиальное решение представляется осью времени (рис.28.1).
По-прежнему будем называть тривиальное решение устойчивым, если для любого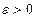 
существует пара величин 
, таких, что из условия 
следует 
для любого t > T.
Если величина 
может принимать любое значение, то система (и невозмущенное движение) называется устойчивым в целом.
Наконец, если
движение называется асимптотически устойчивым.
Рис.28.1. Геометрическая интерпретация
устойчивого тривиального решения.
Запишем теперь (28.4) в скалярной форме, т.е. в виде системы дифференциальных уравнений
, (28.5)
а также продифференцируем по времени функцию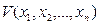 
, имея в виду (28.5),
. (28.6)
Выражение (28.6) называется производной функции V в силу системы (28.5). Компоненты 
можно рассматривать как составляющие вектора фазовой скорости. С другой стороны, градиентом функции V называется вектор
.
Выражение (28.6) можно рассматривать как скалярное произведение вектора градиента функции V на вектор фазовой скорости 
, т. е.(рис.28.2)
. (28.7)
Производная функции V в силу системы (28.5) также является функцией координат вектора состояния. В дальнейшем введем для нее обозначение 
.
Рис. 28.2. Геометрическая интерпретация знака
|
|
|
производной в силу системы уравнений (28.5).
На рис.28.2 показано несколько линий уровня положительно определенной функции V. В малой окрестности начала координат они близки к эллипсам (это становится ясным, если вспомнить формулу разложения в ряд Тейлора функции многих переменных).
С другой стороны из (28.7) видно, что знак производной зависит от угла . В случае, когда угол острый, производная положительна, в случае тупого угла – она отрицательна. На рис.28.2 показан именно последний случай. При этом вектор фазовой скорости направлен вдоль фазовой траектории к началу координат, т.е. величина возмущения стремится к нулю. Это означает, что движение, описываемое уравнениями (28.5), устойчиво.
Подведем итог всему сказанному в виде теоремы Ляпунова об устойчивости.
Теорема.
Если для системы уравнений (28.5) существует знакоопределенная функция V (X), производная которой W (X) в силу системы (28.5) имеет противоположный знак по отношению к V, то решение системы устойчиво.
Доказательство.
Без ограничения общности будем считать функцию V (X) положительно определенной. Выберем 
и положим 
. Обозначим
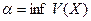
на множестве .
Поскольку 
, то из непрерывности функции V (X) следует существование такого числа > 0, что 
при 
.
Положим теперь, что начальные условия таковы, что 
. Из условия теоремы производная функции V отрицательна вдоль решения 
. Поэтому функция V не может возрастать вдоль этого решения. Следовательно,
. (28.8)
При этом 
. Если предположить, что это не так, то есть найдется 
, тогда
,
что противоречит (28.8). Остается утверждение , что и требовалось.
|
|
|
