 |
Модификация критерия Гурвица для дискретных систем.
|
|
|
|
Выяснить вопрос о наличии или отсутствии условия устойчивости помогает критерий, представляющий собой развитие критерия Гурвица. Итак, рассмотрим систему рекуррентных соотношений вида
. (14.8)
Характеристическое уравнение ее в матричной форме имеет вид
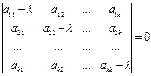. (14.9)
Этот определитель можно записать и в обычной форме алгебраического уравнения степени k, т.е.
.(14.10)
Решение системы (14.8) имеет вид
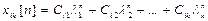, (i =1,2,… k).
Из решения непосредственно следует, что устойчивость его гарантируется при условии |лямбда | < 1. Для того, чтобы воспользоваться известным критерием Гурвица, преобразуем левую полуплоскость корней характеристического уравнения во внутренность окружности единичного радиуса. Это можно сделать при помощи дробно-линейного преобразования вида
. (14.11)
Действительно, положив 
, без труда обнаруживаем
, т.е.
точки окружности переходят в точки мнимой оси и обратно, причем точка лямбда =0 внутренности окружности переходит в точку w = - 1 левой полуплоскости.
Подставив (14.11) в (14.10), после приведения к общему знаменателю и группировки слагаемых с одинаковыми степенями получаем полином степени k, к которому следует применить критерий Гурвица. Если при этом обнаруживается, что Re w < 0, то следствием будет неравенство | λ | < 1.
3.Качественная оценка частоты и амплитуды автоколебаний релейной следящей системы при изменении параметров элементов.
Вначале получим выражения для коэффициентов гармонической линеаризации. Из рис.25.1 видно, что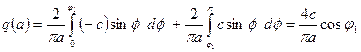 
.
Здесь 
, 2 b – ширина петли гистерезиса, a – амплитуда гармонического сигнала на входе реле. Аналогичным путем находим
Рис.25.1.Прохождение гармонического сигнала
через реле с гистерезисом
|
|
|
.
Далее для построения годографа обратной характеристики нелинейного элемента находим 
.
Как видим, обратный годограф нелинейного элемента представляет собой горизонтальный полубесконечный отрезок с отсчетом амплитуды a вправо (рис.25.2). На этом же чертеже построим годограф линейной части с отрицательным знаком (рис.25.2)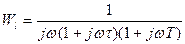 
.
Рис.25.2. Определение параметров автоколебаний
в системе с гистерезисом
Ввиду приближенного характера метода гармонической линеаризации вполне достаточно прочесть значения частоты и амплитуды в точке пересечения годографов линейной и нелинейной частей системы без интерполяции.
Перейдем к исследованию устойчивости автоколебаний с найденными параметрами. При этом полезным оказывается следующее элементарное рассуждение. Предположим, что амплитуда автоколебаний возросла. Тогда годограф линейной части не будет охватывать конец вектора 
и, следовательно, годограф произведения функций в левой части (25.1) не охватит критическую точку с координатами (-1, j .0). Это означает, что система приобрела свойство устойчивости положения равновесия и колебания станут затухать. Однако затухание не приведет фазовую траекторию в начало координат, ибо мы снова придем в точку пересечения годографов. Если допустить уменьшение амплитуды автоколебаний (смещение влево вдоль годографа обратной характеристики нелинейной части), то годограф линейной части охватит критическую точку и система станет неустойчивой, т.е. амплитуда колебаний начнет возрастать. Таким образом, точка пересечения годографов на рис.25.2 соответствует устойчивым автоколебаниям.
При желании уточнить параметры автоколебаний графики на рис.25.2 также оказываются полезными. Кроме того, при качественном построении на годографах может отсутствовать оцифровка по частоте и амплитуде. Тогда, приравнивая мнимые части характеристик согласно уравнению (25.2), получаем условие 
. (25.3)
|
|
|
Решив полученное алгебраическое уравнение, найдем частоту автоколебаний . Приравнивая вещественные части характеристик, найдем соотношение для вычисления амплитуды автоколебаний 
,(25.4)
в которое нужно подставить значение . При решении уравнения (25.3) из нескольких корней необходимо выбрать корень, подходящий по смыслу задачи. Для иллюстрации проделаем вычисления при следующих значениях параметров:
Подставив в (25.3) эти числа, запишем уравнение для вычисления частоты автоколебаний 
с единственным вещественным корнем 
. При этом значении частоты вещественная часть частотной характеристики 
.
Остается решить уравнение (25.4), которое при заданных значениях параметров принимает вид 
с вещественным корнем 0.4055.
Как и следовало ожидать, амплитуда автоколебаний несколько превышает половину ширины петли гистерезиса.
|
|
|
