 |
Преобразование многоконтурных структурных схем.
|
|
|
|
Автоматические системы, структурная схема которых содержит более одного контура называются многоконтурными. В целом ряде задач необходимо уметь преобразовать многоконтурную структурную схему к одноконтурной и мы рассмотрим здесь несколько типичных случаев. На рис.6.6 показана структурная схема с внутренним стабилизирующим контуром с гибкой обратной связью.

Рис.6.6.Следящая система с внутренним стабилизирующим контуром
Преобразование этой схемы к одноконтурной можно выполнить двумя путями. Первый путь состоит в записи передаточной функции внутреннего контура в виде известного нам выражения (6.3).После такого преобразования система становится одноконтурной с жесткой обратной связью (рис.6.7).Передаточная функция при размыкании этой обратной связи записывается в виде
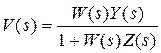 .
.
Второй способ состоит в суммировании передаточных функций Y(s) и
Z(s). Система также становится одноконтурной, но передаточная функция ее при размыкании контура выглядит иначе
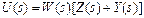
Таким образом, операция преобразования структурных схем может приводить к различным вариантам передаточных функций разомкнутой системы.
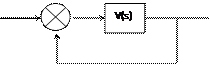 Рис.6.7.Результат преобразования структурной схемы, изображенной на рис.6.6.
Рис.6.7.Результат преобразования структурной схемы, изображенной на рис.6.6.
Рассмотрим еще пример преобразования схемы с перекрестной обратной связью (рис.6.8).
 А)
А) 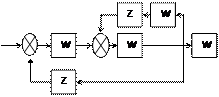 Б)
Б)
Рис.6.8.Преобразование структурной схемы с перекрестной обратной связью.
После получения варианта Б) дальнейшие преобразования сводятся к уже рассмотренным случаям и не требуют комментариев.
Алгоритм поиска минимума интегральной оценки в пространстве параметров.
Уменьшение оценки будем осуществлять подбором параметров tauИ teta корректирующего элемента. Исходя из их допустимых значений, которые определяются рис.12.5, построим начальный симплекс с вершинами в точках с координатами, задаваемыми
|
|
|
| №точки | tau | teta | Интегр.оценка |
| 0.230 | 0.350 | 3.7203 | |
| 0.220 | 1.150 | 1.6862 | |
| 0.086 | 0.710 | 0.1664 |
Из таблицы видно, что наибольшее значение интегральной оценки соответствует параметрам первой точки. Из этой точки делается пробный шаг в новую точку с координатами, вычисляемыми по формулам 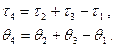
В результате подсчета получаем новое значение интегральной оценки (Табл.13.2)
| № точки | | | Интегр.оценка |
| 0.220 | 1.150 | 1.6862 | |
| 0.086 | 0.710 | 0.1664 | |
| 0.076 | 1.510 | 0.6629 |
Пробный шаг привел к уменьшению интегральной оценки и поэтому принимается. Нетрудно видеть, что геометрически этот шаг соответствует построению отрезка, проведенного из вершины с наибольшей интегральной оценкой через середину противоположной стороны треугольника-симплекса, образованного тремя первоначально выбранными точками. Во вновь образованной таблице «конкурирующими» вершинами оказались две прежних и одна новая. Однако повторение операции с пробным шагом не приведет к положительному результату, ибо новая вершина окажется вне пределов зоны устойчивости (рис.12.5). В этом случае необходимо сократить вдвое длину ребер симплекса, причем вершина с наименьшей интегральной оценкой остается неподвижной. В данном случае такой вершиной служит третья точка. Формулы для вычисления координат двух новых вершин очевидны: 
После подсчета интегральных оценок получаем
| № точки | | | Интегр.оценка |
| 0.086 | 0.710 | 0.16640 | |
| 0.081 | 1.110 | 0.21388 | |
| 0.153 | 0.930 | 0.39266 |
Последующие шаги приводят к постепенному уменьшению интегральной оценки переходного процесса. Остановка всей вычислительной процедуры производится по признаку малого выигрыша в интегральной оценке, которая по принятой терминологии в теории наименьших квадратов является функцией риска. В приведенном примере достаточно малой интегральной оценкой можно считать величину I2 = 0.046608.
|
|
|
|
|
|


