Генерального среднего квадратического отклонения и неизвестного

Значения генерального среднего арифметического

3. Значение генерального среднего квадратического отклонения из­вестно. Значение генерального среднего арифметического известно.

Этот случай довольно часто встречается на практике при контроле постоянно протекающих процессов (транспортировка газа, жидкости и т.п.). Проверка принадлежности к нормально­му распределению для этих условий возможна даже для выбор­ки, состоящей из одного члена. Предположим, что выборка упо­рядочена и представлена в виде (4.62). Значение генерального среднего арифметического обозначим а. Рассчитаем значения:

Если какое-то значение, полученное по зависимостям (4.67), будет больше критических значений β, приведенных в табл. 4.5, то соответствующий результат должен быть исключен.

Таблица 4.5. Предельные значения р для, случая известных значений генерального среднего арифметического и генерального

Среднего квадратического

После оценки наличия грубых погрешностей и исключения содержащих их результатов производят оценку наличия система­тических погрешностей и внесение поправок в результаты измерений. Если во всех результатах содержится постоянная систематическая погрешность, то допускается исключать ее после вычисления среднего арифметического неисправленных резуль­татов наблюдений.

Определение результата измерения и оценка его среднего квадратического отклонения За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения системати­ческих погрешностей.

Несмещенной оценкой генерального среднего арифметиче­ского значения исправленных результатов наблюдений (а) нор­мального распределения является выборочное среднее X, опре­деляемое по формуле (4.63). Несмещенная оценка (Si) для гене­рального среднего квадратического отклонения (α) определяет­ся по зависимости:

Зависимости (4.68) и (4.69) позволяют оценить среднее квадратическое отклонение результата наблюдения.

Среднее квадратическое отклонение S(A) результата измере­ния оценивают по формуле:

Доверительные границы случайной погрешности результата измерения ГОСТ 8.207 установил методику оценки довери­тельных границ случайной погрешности результата измерения для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, то методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

Принадлежность результатов наблюдений к нормальному распределению проверяют с помощью специальных критериев.

Если число результатов наблюдений п > 50, то для проверки принадлежности их к нормальному распределению предпочти­тельно использовать один из критериев: χ² Пирсона или ω² Мизеса — Смирнова.

1. Критерий χ² Пирсона. Результаты наблюдений случайной величины x_i располагают в порядке возрастания (4.62) и вычис­ляют размах х_п — х₁. Размах разбивают на г равных интервалов шириной h:

Число интервалов r выбирают в зависимости от объема вы­борки п. При п = 200 r = 18—20, при п = 400 r = 25—30, при п = 1000 r=— 35—40. Стандарт не рекомендует использовать кри­терий Пирсона при числе наблюдений меньше 200, допуская в исключительных случаях его применение при 100 < п < 200 с количеством интервалов r = 15—18. Однако в работе [10] приво­дятся несколько иные рекомендации. Так, при числе наблюде­ний 50 < п≤ 100 рекомендуемое число интервалов r = 7—9, при 100 < п ≤ 500 r = 8—12, при 500 < n ≤1000 r = 10—16 и при 1000 < п ≤ 10 000 r = 12—22.

Результаты наблюдений группируют по полученным интер­валам и подсчитывают частоты m_j попадания результатов на­блюдений в j -е интервалы.

Затем вычисляются среднее арифметическое значение X и среднее квадратическое отклонение S:

Задаются значением доверительной вероятности того, что величина χ², полученная вследствие случайных отклонений частостей опытного распределения от соответствующих вероятно­стей теоретического распределения, будет меньше значения

(χ *)², установленного для значения доверительной вероятности γ. Для доверительной вероятности γи числа степеней свободы k= r — 1 находят величину (χ*)²/k, вычисляют (χ*)² и сравнивают с ним вычисленную величину χ². Если χ²окажется меньше ( χ *)², то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределений принимается, в про­тивном случае — отвергается.

2. Критерий ω ² Мизеса — Смирнова. Критерий ω² является более мощным, чем критерий χ², но его применение требует выполнения большого количества вычислительных операций. Критерий ω² может быть применен, если число наблюдений превышает 50. Его применение является обязательным, если число наблюдений меньше 200; если число наблюдений более 200, то его применение рекомендуется в случаях, когда результа­ты проверки по другим критериям не позволяют сделать безус­ловный вывод о согласии опытного и теоретического распреде­лений. Например, если при проверке согласия по критерию χ² гипотеза принята при уровне значимости 0,1 и отвергнута при уровне значимости 0,05, то следует дополнительно применить критерий ω ².

Вычисление по критерию ω² проводят в следующем порядке.

Вычисляют значение величины 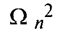по формуле:

Если число результатов наблюдений 50 > п > 15, то для про­верки принадлежности их к нормальному распределению пред­почтительно использовать составной критерий.

1. Составной критерий. Критерий 1. Вычисляют отно­шение d по формуле:

1. 

Значения Р определяются из табл. 4.8 по выбранному уров­ню значимости q* и числа результатов наблюдений п.

При уровне значимости, отличном от представленных в табл. 4.8, значение Р находят путем линейной интерполяции.

В случае если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уро­вень значимости q, а для критерия 2 — уровень значимости q*, то результирующий уровень значимости составного критерия q_Σ<q + q*.

В случае если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Если число результатов наблюдений n≤ 15, то принадлеж­ность их к нормальному распределению не проверяют. Нахож­дение доверительных границ случайной погрешности результата измерения по рассматриваемой нами методике возможно только в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

Доверительные границы ε (без учета знака) случайной по­грешности результата измерения находят по формуле:

Значения коэффициента Стьюдента в зависимости от зада­ваемых значений доверительной вероятности Р и числа резуль­татов наблюдений п приведены в табл. 4.9.

Таблица 4.9. Значения коэффициента t_p,n для случайной величины, имеющей распределение Стьюдента с n - 1 степенями свободы

Доверительные границы неисключенной систематической по­грешности результата измерения Не исключенная систематиче­ская погрешность результата измерения образуется из состав­ляющих, в качестве которых могут быть рассмотрены неисключенные систематические погрешности метода измерения, средств измерений или вызванные другими источниками.

В качестве границ составляющих неисключенной систематиче­ской погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

При суммировании составляющих неисключенной система­тической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величи­ны. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.

Границы неисключенной систематической погрешности 0 результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измере­ний, метода измерения и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле:

При трех или четырех слагаемых Θ_i в качестве значения Θ₁ принимают составляющую, по числовому значению наиболее отличающуюся от других, а в качестве Θ₂ — ближайшую по зна­чению к Θ₁ составляющую.

Доверительную вероятность для вычисления границ неис­ключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной по­грешности результата измерения.

Граница погрешности результата измерения Методика оценки границ погрешности результата измерения зависит от соотно­шения значений случайной и неисключенной систематической составляющих, рассмотренных нами выше. Выделяют три воз­можных случая.

1. Неисключенной систематической составляющей погреш­ности результата измерения можно пренебречь. Необходимым условием для этого является соблюдение неравенства:

На основе (4.83) принимают, что граница погрешности ре­зультата измерения ∆ = ε.

2. Случайной составляющей погрешности результата измере­ния можно пренебречь. Необходимым условием для этого явля­ется соблюдение неравенства:

На основе (4.84) принимают, что граница погрешности ре­зультата измерения ∆= Θ.

При выполнении условий 1 и 2 погрешность оценки вели­чины ∆ за счет пренебрежения значением случайной или неисключенной систематической составляющих не превышает 15%.

3. В случае если неравенства (4.83) или (4.84) не выполняют­ся, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисклю-ченных систематических погрешностей, рассматриваемых в дан­ном случае. Если доверительные границы случайных погрешно­стей найдены в соответствии с (4.80), то допускается границы погрешности результата измерения ∆ (без учета знака) вычис­лять по формуле:

Форма записи результатов измерений При оформлении резуль­татов измерений следует пользоваться рекомендациями МИ 1317.

Если доверительные границы погрешности результата измерения симметричны, то результаты измерений представляют в форме:

Числовое значение результата измерения должно оканчи­ваться цифрой того же разряда, что и значение погрешности ∆.

Если данные о виде функций распределений составляющих погрешности результата измерения и необходимость в дальней­шей обработке результатов или анализе погрешностей отсутст­вуют, результаты измерений представляют в форме:

В случае если границы неисключенной систематической по­грешности 0 вычислены в соответствии с (4.81), следует дополни­тельно указывать доверительную вероятность Р. Значения S(A) и Θ могут быть выражены в абсолютной и относительной формах.

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: