В -. А >.  на. К ». В <. на

В -...    А > ...     на

К »...    В < ...    на

К< ...     на

В + К... А

2. Вставить пропущенные знаки >, < или = одним цветом там, где не нужно ничего вычислять, а затем другим цветом там, где нужно сначала посчитать:

6 + 4... 8 + 5                  А - В... А - С, если В> С

7+ 2... 9-6                   37+ 54... 54+ 37

А + В... А + С                С - А... С - В, если А< В

9 - 4... 8 - 4                   А + К... В + К, если А> В

А + В... В + А               64-1, 7... 64-29

3. Решить задачи:

а) В бутылке было 8 литров кваса. Сколько осталось кваса, если 3 литра выпили?

б) Мешок картошки весит на 7 кг меньше, чем мешок капусты. В мешке капусты А кг. Сколько весит мешок картошки?

в) На станцию доставили А вагонов груза тремя составами. В пер­вом составе было В вагонов, а во втором Д вагонов. Сколько вагонов было в третьем составе?

г) Маме А лет, а сыну В лет. На сколько лет мама старше сына? На сколько сын младше мамы? Сколько лет маме и сыну вместе?

Задание 78. " Совмести фигуры" (развитие внутреннего плана действия)

Учитель предлагает ученику мысленно совместить два данных квадрата. Обращается внимание, что при этом некоторые кружки сов­падут, а некоторые - нет. Нужно определить, как будут расположены несовпадающие кружки после совмещения двух квадратов. В. качестве ответа выбрать один из двух предлагающихся вариантов (2). Выбор ученика анализируется. Затем предлагаются аналогичные задания.

Задание 79. " Передвигай фигуру, не . дотрагиваясь" (развитие внутреннего плана действия)

Перед учеником находится большой квадрат, разделенный на де­вять клеточек. Ученика просят смотреть на фигурку (треугольник,

звездочка, птичка), расположенную в центральной клеточке и мыслен­но ее передвигать на одну клеточку в соответствии с указаниями учи­теля (например, " Вверх, влево, вниз, вправо, вверх, вправо, вниз. Где должна находиться фигурка сейчас? " ). Усложнение задания достигает­ся за счет увеличения количества и скорости передвижения фигурки.

Задание 80. " Запиши правильно"

Записать правильно числа, диктуемые по составу вразбивку. На­пример: а) число, состоящее из семи единиц, одной сотни и пяти де­сятков; б) число, состоящее из девяти единиц и восьми сотен; в) чис­ло, состоящее из шести сотен, четырех единиц и трех десятков; г) число, состоящее из Двух десятков и семи сотен и т. д.

Задание 81. " Раздели на группы " (развитие гибкости мышления) Даются 12-15 арифметических примеров или несколько задач, похожих по математическому содержанию, но разных по способам решения, и разных по внешнему оформлению, но одинаковых по спо­собу решения. Нужно разделить примеры или задачи на группы по каким-либо признакам.

Задание 82.     Формирование понятий " больше", " меньше",

" равно "

1. Подобрать предметы к заданным отношениям:

2. Подобрать два или более примеров по схемам: D = С     и     P> F

3. Обозначить в схеме величины буквами и записать формулы:

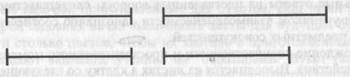
4. Даны формулы: А=В  К< М D> E C< K и схемы к каждой боомуле:

Написать под каждой схемой соответствующую формулу. ' 5. К каждой схеме записать все возможные формулы:

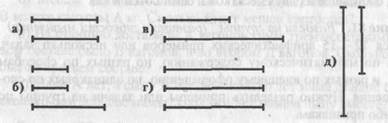
6. К каждой формуле нарисовать схему:

А=В,       C< D,            K> F,            M=N.

Задание 83. Установление взаимно-однозначного соответствия

А. Перед учеником ряд предметов (например, пуговиц). - Задание ученику: " Выложи столько же фишек внизу в ряд, сколько здесь пу­говиц". Если ученик пытается выполнить задание с помощью счета, то нужно показать способ выкладывания фишек в ряд в строгом соот­ветствии с каждым из элементов верхнего ряда и предложить ему продолжить эту последовательность выкладывания. После этого учи­тель закрывает ряд фишек: " Сколько фишек ты выложил? " После от­вета ученика ряд фишек открывается, а в ряду предметов закрывается часть: " Сколько пуговиц закрыто? "

Правильные ответы на поставленные вопросы свидетельствуют о понимании учеником взаимозаменяемости однозначно соотнесенных элементов предметных совокупностей.

Б. Расхождение количественного и пространственного моментов в условиях действия. Выполняется на листах в клетку со следующей за­готовкой:

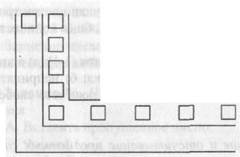
Ученику предлагается дорисовать квадраты на пустой дорожке, чтобы их было столько же. сколько квадратов на первой дорожке. Отмечается знаком " +" действие с ориентацией на количественное соотношение элементов множеств, знаком " -" - действие с ориента­цией на пространственное расположение элементов.

В. Сравнение множеств, элементом одного из них является от­дельный предмет, а элементом другого множества - сразу несколько I предметов.

Выполняется на листах со следующей заготовкой:

Задание: " В верхней части листа - ваза с букетом цветов. Ниже -пустые вазочки, приготовленные для букетов. Под ними клумба, на которой садовник начал высаживать цветы для будущих букетов. На­рисуй столько цветов, чтобы их хватило в приготовленные вазочки". Обращают внимание ученика на " образцовый" букет (какой букет должен получиться), не называя при этом количество цветов в букете.

Фиксируются следующие способы действий:

" +" - способ соотнесения ваза- букет (1-3): рисунки цветов трой­ками, пространственно отделенными друг от друга; общее количество цветов в этом случае будет равно 12;

" -" - способ поединичного соотнесения ваза- цветок (1-1): а) в этом случае на рисунке будет изображено всего 4 цветка; б) непринятие условия задачи: произвольное рисование цветов; в) пока есть свобод­ное место.

Задание 84. Присчитывание и отсчитывание предметных сово­купностей

A. На длинной бумажной ленте наклеены на одинаковом расстоя­нии друг от друга 6 маков. Заготовлена еще одна лента с 4 маками. Перед учеником кладется первая лента и предлагается сосчитать пальцем имеющиеся на ней цветы. Затем учитель меняет положение ленты так, что ее правый конец теперь находится слева. После того как ученик заверяет, что на ленте " все равно 6 маков", к ней придви­гается вторая лента, и ученика спрашивают: " Сколько всего цветков теперь перед тобой? " Фиксируется, продолжит ли ученик считать дальше (т. е. будет присчитывать) или начнет считать цветы заново (пересчитывать).

Б. Перед учеником кладется длинная бумажная лента с 11 квадра­тами - " улица, на которой расположены дома". Учитель показывает начало и направление счета и говорит: " Вот этот домик (делается ука­зание)- девятый. Скажи, а какой по счету будет этот домцк? " (Ука­зывается шестой). Отмечается, в каком направлении ученик будет вести счет: в прямом, начиная с далекого первого домика, или в об­ратном, начиная с близкого девятого.

B. Перед учеником ряд кубиков. Левая часть ряда закрыта. Учи­тель указывает на первый после экрана кубик: " Это шестой кубик. Сколько кубиков спрятано? "

Задание 85. Математический диктант (умение разбивать вто­рое слагаемое на удобные для вычисления части)

А. Записано число 8. Как к нему прибавить 6? 7? 5? и т. д. По ходу называния чисел ученик записывает: 2+4, 2+5, Z+3 и т. д.

Записано число 7. Как его прибавить к числу 8? 6? 9? В этом зада­нии части числа 7 всякий раз оказываются разными: 2+5, 4+3, 1+6.

Б. Записать вычитаемое в виде удобных для вычисления частей.

Записано число 8. Как вычесть его из 15? 13? 16? Ученик записы­вает: 5+3, 3+5, 6+2.

Записано число 13. Как из него вычесть 8? 5? 7? Первая часть всех записей должна быть одинакова: 3+5, 3+2, 3+4.

Задание 86. Понимание взаимосвязи операций сложения и вычи­тания

A. Вставить пропущенное число: 9-. = 6

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: