АхВ=С В +С С:А В:С  ВхА  В:А  С:В

. -5 = 2 3 +. = 10

Б. Дается запись состава чисел: 95 -*; —---- 17

^^-\ 78

и примеры, составленные на основе первой записи: 95-17 = 17 + 78 = 95 - 78 = 78-17 = 95 + 17 =

Два последних примера намеренно составлены неправильно, но ученик об этом не предупреждается. Там, где ученик не знает ответ, нужно поставить знак вопроса.

B. Понимание зависимости изменения результата арифметическо­го действия от изменения одного из его-компонентов:

a) 3 + k = 8 б) z + 6 => 13 в) 10 - Р = 3   г)а-3 = 9 4 + к=.          z + 5 =.        9-0 =.        а-4=.

Учитель: " Догадайся, какое число должно стоять в ответе. Для этого надо внимательно посмотреть на первую строчку, подумать, а потом сказать ответ". Отмечаются:

- нахождение значения абстрактного элемента в первом примере и подстановка его значения во второй пример;

- решение на основе понимания функциональной зависимости из­менения результата арифметического действия от изменения одного из его компонентов;

- направление изменения искомой величины выбрано ошибочно;

- перевод абстрактного обозначения в обычные числа по внешне­му сходству: а = 2, р = 3, z = 7 и т. д.

- выбор какого-либо формального правила и действия по этому Правилу во всех случаях.

Задание 87. Понимание связи между компонентами сложения и вычитания, умножения и деления

А. Ученику нужно соединить линиями разного цвета слова, одина­ковые по смыслу. Эти же слова учитель может написать на отдельных карточках и попросить ученика разложить их на группы: одинаковые и разные по смыслу.

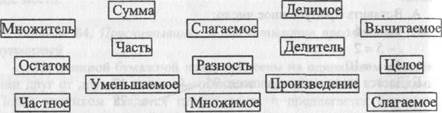
Б. Ученику дан пример с ответом. Учитель записывает новые при­меры, которые " один ученик" якобы составил на основе исходного примера. Учащемуся предлагается оценить их правильность и выпи­сать только те из них, которые составлены правильно, а у неправиль­но составленных в качестве ответа ставить вопросительный знак.

6+2=8        8-2=        2+6=          8-6=

10-7=3        10-3=       7 + 8=          3 + 7 =

15 + 27 = 42    42 - 15 =        27 + 15 =          42 - 27 =

51-13 = 38      38 + 13=        51+38=          51-38 =

6-2=        6-8=

7-3=        3-10 =

27-42=     27-15*

13 + 38=       38-13 =

А+В=С С-А=  В+А-   В-С=  С-В=  В-А=

А-В = С В + С=   А+С=   С+В=   А-С =   С-В =

В. Ответ к новому примеру взять из основного:

15x5 = 75 75: 5= 15: 75= 75: 15= 75-15= 5x15=   15: 5=

98: 7=14 14x7= 14: 98= 98: 14= 98-14= 7x14=     14: 7=

АхВ=С В +С С: А   В: С    ВхА    В: А     С: В

А: В= С СхВ А-С   СхВ   С: В     А: С     ВхС

Задание 88. Понимание смысла счетного действия А. Умение правильно соотносить число и предметы без пропусков и пересчитывания дважды. Нужно подсчитать предметы, располо­женные по разным конфигурациям.

Б. Понимание учеником независимости количественного результа­та от направления счета. Ученику предлагается карточка с изображе­нием ряда предметов, расположенных в убывающей последователь­ности. Учитель: " Это оставленные на вешалке шляпы гостей. Сколько людей пришло в гости? "

После ответа ученика карточка переворачивается так, что после­довательность предметов становится возрастающей. Учитель: " А те­перь сколько гостей в доме? '¹

Отмечается, пересчитывает ли ученик заново предметную сово­купность или нет.

Задание 89. Овладение числовым рядом и его свойствами А. Ученику предлагаются задания на:

прямой счет (сосчитать до 10, начиная с 3, 5, 8; сосчитать до 30, ¹ начиная с 21, 24, 27; сосчитать до 70, начиная с 62, 66, 69; сосчитать от 90 до 100, от 193 до 203, от 999 до 1003, от 3141 до 3151;

обратный счет (сосчитать от 10 до 1, от 30 до 20, от 72 до 62, от 101 до 91, от 203 до 193, от 1003 до 999, от 3151 до 3141).

Отмечаются: а) все случаи, когда ученик, чтобы начать обратный счет, сначала обращается к прямому счету; б) сравнить легкость и скорость обратного счета и прямого счета; в) на каком уровне обрат­ный счет еще безошибочен; г) различия в уровнях прямого и обратно­го безошибочного счета.

Б. Задания ученику:

а) считай с " а" до тех пор, пока не станет на " п" больше: п=2, 5, 8 а=3, 7, 14;

б) считай от " а" до " Ь" и скажи, сколько единиц ты насчитал: а=3                    Ь=7

а=4                    Ь=10

а=9                    Ь=19

в) начни считать в обратном порядке от " Ь" до тех пор, пока не бу­дет на " п" меньше:

Ь=3                        п=2

Ь=7                        п=5

Ь=14    п=8

г) считай от " Ь" до " а" в обратном порядке и скажи, сколько еди­ниц ты насчитал:

Ь=7                    а=3

Ь=10                  а=4

Ь=19                  а=9

Фиксируется: 1) количество правильных ответов при прямом и об­ратном порядке; 2) какие средства употребляет ребенок - считает на пальцах, откладывает предметы; 3) паузы, задержки; количество включений прямого счета при обратном счете.

В. Дан " сказочный" пример с одним " обычным" числом:

А + 1 = В. Из двух " сказочных" чисел подчеркните большее. Объ­ясните свой выбор.

С- 1 = Р. Из двух " сказочных" чисел подчеркните то, которое в сказочном числовом ряду стоит правее.

К + 2 = Е, П - 1 - Р. В каком из этих двух примеров использованы последующее и предыдущее " сказочные" числа? (во втором).

Г. Учитель записывает: ВСРБТНи предупреждает, что все эти " числа" написаны по порядку. Но самое первое число - это не 1. Где какое число, нам неизвестно. Зная это, нужно записать: самое боль-

шое из записанных чисел - Н; число, которое меньше самого большо­го на 1, - Т; самое маленькое число - В; число, большее, чем это са­мое маленькое, на 1, — С. Сравнить числа С и Р, Р и Т и записать, на сколько одно меньше другого (на 1 и на 2).

Задание 90. Усвоение различий между числом и цифрой

A. Сравнить " сказочные" числа: КС... К; 9... PC; КЗ... К4; 5Н... ЗН; КАВ... КАО; ЗКЕ... 5ОР

Б. Записать три заданных числа по порядку от большего к мень­шему:

К7Г, К8Р, К80

B. Записать " сказочные" числа в виде суммы разрядных слагае­мых, записывая ноль обычным способом (в скобках приводятся ожи­даемые от учащихся решения):

АКС = (А00 + K0 + C)     ПОР = (П00 + Р)    EB0 = (Е00 + ВО)

Г. Дается сумма разрядных слагаемых. Нужно записать разложен­ное число:

В0О + КО + Т (ВКТ)

П00 + П (ПОП)

Р00 + ВО

(РВО)

коо + ко + к

(ККК)

Задание 91. Составить примеры (анализ через синтез) Заполнить пропуски:

A. ... +... = 5         ... +.,. = 6   .. ". +... = 8... +... = 5            ... +.. '. = 6   ... +... = 8

... +... = 6   ... +... = 8... +... = 8

Б. 7 + 2< 7 +...                           ... + 4< 4 +...

5-... = 5-...                               ... -3<... -3

6 +... > 6 +...                             ... + 3 = 3 +...

B. 8... 3-5                                4... 3= 12 10... 5 = 2                                   12... 4= 16

9... 3 = 27                                   18... 6 = 3

24... 8 = 32                                 18... 6 = 12

Задание 92. Понимание разницы между количественными и по­рядковыми числительными

1. Нарисовать десять кружков. Зачеркнуть: а) три кружка, семь кружков; б) третий кружок, седьмой кружок.

2. Нарисовать флажок между четвертым и пятым кружками и т. д.

Задание 93. Арифметические задачи

A. Задачи на расхождение сюжетного и арифметического дейст­вий.

- Из класса вынесли 7 стульев, потом вынесли еще 4 стула. Сколь­ко стульев вынесли из класса?

- Дети играли в кубики. Витя добавил Кате 4 кубика из своей ко­робки. Сначала у него в коробке было 16 кубиков. Сколько их те­перь?

Б. Задачи с недостающими данными.

- На ветке сидели вороны, 4 вороны улетели. Сколько осталось?

- Тане подарили 2 книги, а Кате - 3. Сколько книг стало у Тани?

B. Задачи с лишними данными.

- В ящике было 15 кг яблок, а в мешке - 30 кг. Из ящика продали 5 кг яблок. Сколько яблок осталось в ящике?

- Сережа сделал 20 закладок. В классе он раздал 10 закладок, а во дворе - на 3 закладки меньше. Сколько закладок он раздал ребятам во дворе?

- В школьную библиотеку пришли 15 учеников. Из них-7 учени­ков взяли по 3 книги каждый, а остальные ребята только сдали книги. Сколько всего книг ученики взяли в библиотеке?

Задание 94. Задачи на сообразительность

А. В корзине лежит 5 яблок. Как разделить эти яблоки между пя­тью девочками, чтобы каждая, девочка получила по одному яблоку и чтобы одно яблоко осталось в корзине?

Б. На столе лежат три спички. Не прибавляя ни одной спички, сде­лайте из трех - четыре. Ломать спички нельзя.

Задание 95. Задачи на вычленение математического содержания А. Волк пригласил на свой день рождения Р поросят, К козлят и

Д Красных Шапочек. Сколько аппетитных гостей пригласил Волк на

свой день рождения?

Б. В автобус вошли 7 бабушек. Двум из них уступили место. Скольким бабушкам пришлось стоять? Сколько воспитанных пасса­жиров ехало в автобусе?

В. С одного дерева сняли В груш и двух мальчиков, которые съели по С груш каждый. Сколько всего груш было на дереве, на которое тайком залезли мальчики и съели чужие груши?

Использованная литература

1. Акимова М. К., Козлова ВТ. Коррекционно-развивающие уп­ражнения для учащихся 3-5 классов. Обнинск, 1993 (задание 206)

2. Александрова Э. И. Математика. Учебник для I класса. (Про­грамма развивающего обучения). Харьков - Москва. 1994 (задания 3, 77, 82, 87а, 91, 94, 95).

3. Артемов А. К. Трудности, возникающие у детей при обобщении в математике. // Начальная школа. 1982. № 4. С. 32-34.

4. Афанасьева Л. Г. Зрительные диктанты на уроках математики. // Начальная школа. 2000. №7. С. 100-102 (задание 76).

5. Безруких М. М., Ефимова СП. Упражнения для занятий с деть­ми, имеющими трудности при обучении письму. М., 1991 (задания 2а, 5, 40, 41).

6. Бирюкова Л. А. Прием классификации при обучении математи­ке. // Начальная школа. 1988. № 5. С. 36-39 (задание 19).

I. Боденко Б. Н. Выявление некоторых причин трудностей в уче­нии. // Научно-практические проблемы школьной психологической службы. М., 1987. T. I. C. 78-81 (задание 6).

8. Боденко Б. Н. Реализация психологического содержания теста Керна- Иирасека в диагностической практике. // Научно-методичес­кие основы использования в школьной психологической сдужбе кон­кретных психодиагностических методик. М., 1988. С. 35-47 (зада­ние 7).

9.  Бондаренко СМ. Почему детям трудно учиться? М., 1976. Вып. 2 (задание 16).

10. Боровик О. Развитие воображения. Методические рекоменда­ции. М., 2000 (задание 52). .

II. Бугрименко Е. А., Цукерман Г. А. Чтение без принуждения. М., 1987 (задания 34а, 39).

12. Гальперин П. Я., Кабыльницкая С. Л. Экспериментальное фор­мирование внимания. М., 1974. (задание 10).

13. Грушевская М. С. Нарушения письма у младших школьников. // Начальная школа. 1984. № 6. С. 35-36.

14. Даминова М. П. Как можно помочь ученику избавиться от " прочих" ошибок. // Начальная школа. 1988. № 5. С. 15-18.

15. Диагностика умственного развития дошкольников. / Под ред. Л. А. Венгера и В. В. Холмовской. М., 1978 (задание 11).

16. Заика Е. В. Упражнения для формирования навыка чтения у младших школьников. // Вопросы психологии. 1995. № 6. С. 43-54 (за­дания 32, 46, 50, 53-62, 64, 65, 68-74).

17. Зак А. З. Просвет и другие интеллектуальные игры для детей 6-10 лет. М., 1993 (задание 78).

18. Зак А. З. Методы развития интеллектуальных способностей у детей 8 лет. М., 1994 (задание 256).

19. Засорина Л. Н., Плюснина Е. М., Данилова Н. В. Навыки громко­го чтения (контроль и методика отработки). С. -П., 1996 (задания 37, 38, 49).

20. Зинченко С. Н. Почему детям бывает трудно учиться. Киев, 1990.

21. Иваненко С. Ф. К диагностике нарушений чтения и письма у младших школьников. //Дефектология. ⁰1984. № 1. С. 52-55.

22. Изучение развития учащихся 'учителем (Методические реко­мендации для учителей начальных классов). / И. И. Аргинская и др. М., 1985 (задание 1).

23. Костромина Н. И., Костромина М. Э. Развитие орфографиче­ской зоркости и бокового зрения через зрительные диктанты. // На­чальная школа. 2001. №3. С. 58-61. (задание 45).

24. Локалова Н, П. Виды анализа учебного материала и психологи­ческие трудности при их несформированности. // Начальная школа.

994. №5. С54-59.

25. Локалова Н. П. Как преодолеть медленное чтение у школьни-: ов. // Начальная школа (Приложение к газете «Первое сентября»). 998. №18. С. 4.

26. Методы 'обследования нарушений речи у детей. / Под ред. . А. Власовой. М., 1982 (задания 26, 28, 29).

27. Практические занятия по психологии / Под ред. А. В. Петров-: кого. М., 1972 (задания 26, 22).

28. Практикум по психологии / Под ред. А. Н. Леонтьева, Ю. Б. Гип-[енрейтер. М., 1972 (задания 17, 21).

29. Рабочая книга школьного психолога. / Под ред. И. В. Дуброви­ной. М., 1991 (задания 20а, 24)

30. Романова Е. С., Усанова О. Н., Потемкина О. Ф. Психологиче­ская диагностика развития школьников в норме и патологии. М., 1990 (задание 13).

31. Руководство по оценке качества математических и лингвисти­ческих знаний школьников. / Отв. ред. В. И. Слободчиков. М, 1989 (задания 83-86, 876, 88, 90).

32. Соколовская СМ. Словарь в ребусах (для 1 - 3 классов). Раз­вивающее обучение. М., 1994 (задание 51).

33. Соловьева З. И. Приемы работы по предупреждению у учащих­ся орфографических ошибок. // Начальная школа. 1985. № 3. С. 59-61.

34. Сорокун П. А. Формирование и развитие пространственных представлений у учащихся. Автореферат дисс. докт. психол. наук. Л., 1968 (задание 33 (№№ 8, 9).

35. Ульенкова У. В. Исследование психологической готовности шестилетних детей к школе. // Вопросы психологии. 1983. № 4. С. 62-69 (задание 9).

36. Фомина Л. Н. Материалы к урокам чтения. //Начальная школа. 2001. №2. С. 102-104. (задание 63).

37. Чудесная газета. 2001. №1. (задание 33).

38. Эльконин Д. Б. Развитие устной и письменной речи учащихся. М., 1998 (задание 47).

СОДЕРЖАНИЕ

Предисловие автора к третьему изданию............................................ 3

Предисловие автора ко второму изданию............................................ 4

Введение................................................................................................... 5

Раздел I. Основные группы трудностей при обучении

младших школьников русскому языку, чтению,

математике и их психологические причины....................... 8

Раздел II. Психодиагностические таблицы........................................ 14

Таблица 1. Трудности при обучении русскому языку:

психологические причины, диагностика и коррекция..... 14

Таблица 2. Трудности при обучению чтению:

психологические причины, диагностика и коррекция..... 27

Таблица 3. Трудности при обучении математике:

психологические причины, диагностика и коррекция..... 35

Раздел III. Задания для психодиагностики причин

выявленных трудностей и их устранения.......................... 44

Использованная литература.................................................................. 92

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: