 |
RL-подход к динамической Q-маршрутизации
|
|
|
|
Динамическим аналогом традиционных алгоритмов статической (фиксированной) маршрутизации является так называемый алгоритм Q-маршрутизации (Q-routing) [18]. Этот алгоритм динамической маршрутизации основан на RL (Reinforcement Learning), подходе, использующем распределенный механизм оценки стоимостей маршрутов в динамических ТКС. Опишем этот алгоритм подробнее.
Алгоритм Q-маршрутизации потоков данных является модификацией алгоритма маршрутизации Беллмана-Форда [17]. Он эффективно работает как в статических, так и в динамических ТКС с высоким риском сетевых перегрузок.
Алгоритм является распределенным, так как выполняется в каждом узле ТКС. Он производит итеративные (рекуррентные) вычисления для определения и корректировки маршрутов, близких к оптимальным. При этом используется функционал, оценивающий стоимость маршрутов передачи пакетов данных в глобальных ТКС.
Особенность алгоритма заключается в том, что в каждом узле ТКС для каждого узла-получателя определяется не весь маршрут, а только соседний узел, которому нужно переслать пакет. Таким образом, рекуррентный алгоритм Q-маршрутизации вычисляет локально- оптимальные маршруты. При этом не гарантируется глобальная оптимальность синтезированных маршрутов.
Задача Q-маршрутизации в динамических ТКС формулируется следующим образом.
Пусть заданы:
G(A(t),R(t),W(t)) – ориентированный граф ТКС;
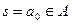– узел-источник пакетов данных;
– стоимость ребра 
, удовлетворяющая естественным соотношениям:
w(i,i) =0; 
, если узлы i и j не соединены
, если узлы i и j соединены;
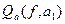– функционал стоимости маршрутов, соответствующий оценке узлом 
стоимости маршрута, содержащего ребро 
, до узла-получателя 
.
Требуется построить локально-оптимальные маршруты от узла-источника 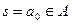до остальных узлов , позволяющие на каждом шаге минимизировать стоимость каналов связи ТКС.
|
|
|
Решение этой задачи разбивается на два этапа:
- прокладка начальных маршрутов
- корректировка маршрутов.
Опишем вычислительную работу алгоритма на каждом этапе.
1-й этап (прокладка начальных маршрутов)
Вычисление начальных маршрутов можно осуществить с помощью алгоритма Беллмана-Форда. По окончании работы этого алгоритма значения функционала стоимостей определяются по следующей формуле:
, (3.4.1)
где L(v,f) – стоимость кратчайшего маршрута от узла v до узла f.
На данном этапе главный интерес представляют не столько сами начальные маршруты (их можно и не запоминать), сколько получение начальных значений функционала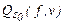 
.
2-й этап (корректировка маршрутов)
На каждом шаге алгоритма происходит обновление оценок стоимостей по рекуррентной формуле
), (3.4.2)
где 
– «коэффициент обучения» (обычно выбирается m =0.5), а lk(f,v) вычисляется по формуле:
. (3.4.3)
Технология прокладки маршрута с помощью описанного алгоритма заключается в следующем
При передаче пакета данных узлу-получателю f узел-источник s0 сначала пересылает его к соседнему узлу v=a1, на котором значение функции 
минимально. Затем этот узел a1 пересылает пакет узлу v =a2, на котором достигается минимум функции 
и т.д. до тех пор, пока пакет данных не придет в заданный узел-получатель f.
Эффективность алгоритма Q-маршрутизации зависит от выбора коэффициента обучения μ. При значениях m, близких к 1, возрастает риск возникновения так называемых «узких мест», т.е. возможность появления маршрутов, совместно используемых для передачи пакетов данных несколькими парами “источник-получатель”.
Заметим, что если маршрут оптимален, то любой содержащийся в нем подмаршрут тоже оптимален. Таким образом, если несколько пар «источник-получатель» будут передавать пакеты данных только по оптимальному маршруту, то это с большой вероятностью приведет к перегрузке соответствующих каналов связи ТКС.
|
|
|
При значениях “коэффициента обучения” m, близких к 0, изменения стоимостей маршрутов будут мало влиять на решение. В этом случае вычисляемые по алгоритму маршруты могут быть достаточно далеки от глобально оптимальных.
Экспериментальные исследования показали, что распределенный алгоритм Q-маршрутизации достаточно легко адаптируется как к возможным изменениям структуры (топологии) параметров динамических ТКС, как и к возможным изменениям направлений передачи и интенсивности потоков данных.
На рис.3.4.1. приводится сравнительная характеристика алгоритмов Q-маршрутизации (Q-routing) и OSPF-алгоритма (Shortest Path), полученная в работе [18]. Ось абсцисс на приведенной диаграмме соответствует средней загрузке сети, ось Y - среднему времени доставки пакетов данных.
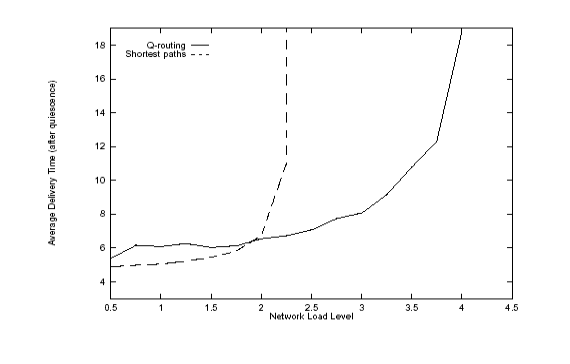
Рис.3.4.1. Сравнительная оценка эффективности работы алгоритмов Q-маршрутизации и OSPF
Как видно из рис. 3.4.1, при увеличении нагрузки на сеть алгоритм Q-маршрутизации оказывается более устойчивым, чем алгоритм OSPF, который является стандартом в современных ТКС.
|
|
|
