Критерий маршрутизируемости

Пусть ТКС задана своей графовой моделью, т.е. орграфом G(A,R,W). Назовем простой таблицей маршрутизации τ_i узла a_i Î A отображение множества узлов A ТКС на множество узлов-соседей A_i Î A узла a_i, т.е.

(3.3.1)

С каждым узлом ТКС a_i Î A свяжем локальную БД и локальную БЗ маршрутизации. БД определяется как результат отображения τ_i, т.е. набором пар узлов из A_i × τ_i (A_i)), а БЗ - как само отображение τ_i. Это позволяет учитывать в БЗ дополнительные характеристики ТКС, такие как топология сети, стоимости каналов связи и т.п.

Таблицы маршрутизации, реализованные в локальных БД узлов ТКС, могут строиться с помощью БЗ в соответствии с некоторым критерием оптимальности (например, минимизация суммарной стоимости маршрута) на основе экспертных или иных решающих правил (тогда множество параметров, учитываемых при выборе маршрута, может быть расширено) или задаваться напрямую администратором сети. Примером таких таблиц могут служить простые таблицы маршрутизации стандартного вида.

Пусть для каждого узла ТКС задана связанная с ним БД – простая таблица маршрутизации. Назовем множество таких таблиц простой картой маршрутизации ТКС. Формально карту маршрутизации глобальной ТКС можно представить в виде

. (3.3.2)

Карта маршрутизации T может быть реализована как распределенная по узлам ТКС БД, представляющая собой совокупность таблиц маршрутизации. При этом не производится предварительная (априорная) прокладка маршрутов от одного узла ТКС к другому, а осуществляется только определение соседей для каждого узла ТКС.

Управление потоками данных будет производиться на основе таблиц маршрутизации на передающих узлах, каждая их которых будет определять выбор следующего узла маршрута. В этом случае сам маршрут передачи данных от одного узла ТКС к другому будет являться результатом только распределённого сетевого управления.

Настройка таблиц маршрутизации должна будет осуществляться так, чтобы конечный маршрут передачи данных был корректным и соответствовал накладываемым на него ограничениям на пропускную способность каналов связи и пропускную способность узлов ТКС и заданным требованиям (например, минимизация стоимости маршрутов). Заметим, что пропускная способность узла ТКС определяется, исходя из пропускной способности его каналов связи и размера (объёма памяти) буфера узла для пересылаемых пакетов данных.

Если карта маршрутизации T будет реализована как глобальная БД маршрутизации ТКС, которая может храниться в памяти маршрутизатора-координатора, то этап прокладки маршрутов будет осуществляться агентом-координатором. Агент-координатор на основе карты маршрутизации и глобальной БЗ сам проложит по таблицам маршрутизации необходимый (например, оптимальный) маршрут от узла-источника к узлу-получателю и вернет его запрашивающему агенту-узлу.

В обоих случаях сетевое управление прокладкой маршрута ведётся следующим образом: фиксируется узел-получатель данных f и для него от узла-источника s последовательными отображениями строится последовательность узлов ТКС вида

s=a₀, a₁, a₂, …, a_k=f, (3.3.3)

таких, что для любого i =1, 2, …, k справедливо соотношение τ_i-1(f)=a_i.

Карту маршрутизации ТКС и соответствующую ей БД будем называть корректной, если по ней можно проложить маршрут передачи данных между любыми двумя узлами графа G(A,R,W).

Критерий, позволяющий прокладывать с помощью карты маршрутизации маршруты передачи пакетов данных между любыми двумя узлами ТКС, будем называть критерием коммуникабельности (маршрутизируемости) ТКС.

Основываясь на глобальной БД, реализующей карту маршрутизации ТКС, этот критерий можно сформулировать в виде следующей теоремы.

Теорема 3.3.1. Карта маршрутизации ТКС корректна, т.е. для любого узла-источника данных s и любого узла-получателя данных f из множества A узлов ТКС существует последовательность узлов вида (3.1.3) такая, что

для всех i=1,2,…,k, (3.3.4)

тогда и только тогда, когда для любого узла и для любого разбиения множества A на непустые подмножества A₁ и A₂, такие, что 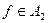, найдутся узлы и , для которых справедливо соотношение

τ₁(f)=a₂. (3.3.5)

Для доказательства теоремы 3.3.1 сначала покажем, что из второго утверждения следует первое. Зафиксируем узел-получатель . Рассмотрим любое разбиение множества узлов на подмножества A₁ и A₂, где 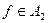. Возьмем любой узел из подмножества A₁ и обозначим его через s. Тогда существует последовательность узлов вида (3.3)такая, что для любого i=1, 2,..., k верно, что τ_i-1(f)=a_i. 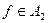Так как узел-источник , а узел-получатель , то существует такой индекс j, что

, и τ_j-1(f)=a_j. (3.3.6)

Таким образом, требуемая импликация доказана.

Покажем теперь справедливость обратной импликации, т.е. докажем, что из первого утверждения теоремы следует второе. Зафиксируем узлы . Разобьем множество узлов A на подмножества A₁⁽⁰⁾ и A₂⁽⁰⁾, причем A₂⁽⁰⁾ ={ f }. Тогда существует такой узел , что τ₁(f)=f. Если 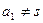, то разобьем множество A на подмножества A₁⁽¹⁾ и A₂⁽¹⁾, где A₂⁽¹⁾ ={ f, a₁ }. Тогда существует такой узел , что . Если , то продолжим построение последовательности узлов до тех пор, пока не получим a_k=s. Заметим, что для всех подмножеств A₂⁽ⁱ⁾ верно, что из любого узла этих подмножеств существует маршрут до узла-получателя f, определяемый таблицами маршрутизации ТКС. Поскольку 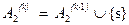, то между узлом-источником s и узлом-получателем f существует маршрут, определяемый таблицами маршрутизации. Следовательно, обратная импликация также справедлива.

Таким образом, теорема 3.3.1 доказана. Она определяет необходимое и достаточное условие коммуникабельности (маршрутизируемости) ТКС в терминах корректности карты маршрутизации.

Важно отметить, что таблицы маршрутизации определяют только один маршрут между узлом-источником s и узлом-получателем f. В противном случае существовали бы такие таблицы t_i ÎT и узлы a Î A, для которых справедливы соотношения

, (3.3.7)

что противоречит определению простых таблиц маршрутизации для узлов ТКС.