Метод оптимальной маршрутизации, основанный на построении остова минимальной стоимости графовой модели ТКС

Задача статической маршрутизации для остовного алгоритма полагает, что в качестве решения задачи маршрутизации алгоритм прокладывает от заданного узла-источника до каждого узла-получателя ТКС ровно один маршрут. При этом структура ТКС считается фиксированной, т.е. не изменяющейся с течением времени, и не учитываются такие параметры, как интенсивность потоков данных и текущая загрузка каналов связи ТКС.

Постановка задачи оптимальной маршрутизации пакетов данных в статических (фиксированных) ТКС для остовного алгоритма следующая. Пусть статическая модель ТКС представлена графом G(A,R,W) и задана пара узлов , первый из которых является узлом-источником, а второй – узлом-получателем. Требуется найти маршрут передачи пакетов данных из s в f минимальной стоимости.

Так как любой подмаршрут оптимального маршрута является оптимальным, то для решения задачи оптимальной маршрутизации достаточно построить дерево кратчайших маршрутов для каждого узла-источника 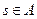. В случае симметричных статических ТКС, у которых веса каналов связи (ребер графа) одинаковы в обоих направлениях и не изменяются с течением времени, любое дерево кратчайших маршрутов для одного узла будет деревом кратчайших маршрутов для всех остальных узлов. Это означает, что в симметричных ТКС задача оптимальной маршрутизации сводится к задаче построения остова минимальной стоимости, т.е. максимального связного подграфа T графа G, не содержащего циклов, сумма стоимостей ребер которого минимальна.

Рассмотрим алгоритм построения такого остова.

Работа алгоритма:

Алгоритм выполняется итеративно за конечное число шагов. Сначала выбираем произвольный узел 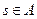и полагаем, что

T =({ s }, Ø, W). (2.3.4)

Шаг алгоритма: выбираем ребро с минимальным весом такое, что его начальный узел, принадлежит графу T, а конечный узел – не принадлежит T, и добавляем его вместе с конечным узлом в T, т.е.

. (2.3.5)

Алгоритм выполняется до тех пор, пока в T не войдут все вершины графа G.

Теорема 2.3.1: Граф T, построенный по остовному алгоритму, будет остовом минимальной стоимости графовой модели G симметричной статической ТКС.

Для доказательства этой теоремы потребуется следующая лемма.

Лемма 2.3.1: Для любого узла a_i Î A графа G(A,R,W) симметричной ТКС инцидентные ему ребра (a_i, a_j)Î R минимальной стоимости содержатся в графе T вида (2.3.4), (2.3.5).

Доказательство леммы 2.3.1: При построении графа T возникает два случая, когда на очередном шаге алгоритма существует возможность включения ребра (a_i, a_j) в T:

1) ;

2) .

Рассмотрим первый случай. Так как a_i принадлежит T, то либо a_i = s (тогда согласно (2.3.5) ребро (a_i, a_j) будет включено в T на первом шаге), либо на каком-то шаге узел a_i включен в T вместе с ребром, чья стоимость, с одной стороны, меньше стоимостей всех остальных ребер, которые не принадлежат T и инцидентны узлам, входящим в T, а, с другой стороны, – больше, чем стоимость ребра (a_i, a_j). Тогда из (2.3.5) следует, что ребро (a_i, a_j) будет включено в T на следующем шаге.

Во втором случае будем рассматривать шаг алгоритма, на котором в T будет включен узел a_i. Согласно (2.3.5) этот узел войдет в T вместе с ребром (a_i, a_j), так как его стоимость среди всех инцидентных a_i ребер – минимальна.

Таким образом, лемма 2.3.5 доказана.

Доказательство теоремы 2.3.5. Так как граф G симметричной ТКС – связный, то на каждом шаге алгоритма множество ребер, начало которых принадлежит T, а конец – нет, будет непустым. Таким образом, процесс построения не закончится, пока в T не войдут все вершины графа G.

Так как на каждом шаге алгоритма к графу T добавляется по одному узлу и одному ребру, а в начале он содержит только один узел и одно ребро, то в конце он будет состоять из N узлов и N-1 ребра (где N – число узлов в графе G). Это означает, что T будет остовом графовой модели G ТКС. Докажем, что его стоимость будет минимальной.

Рассуждая от противного, предположим, что существует остов T¹ такой, что сумма весов его рёбер меньше суммы весов рёбер остова T. Тогда справедливо соотношение

. (2.3.6)

Однако это соотношение противоречит утверждению леммы 2.3.1. Следовательно, соотношение (2.3.6) неверно и стоимость T действительно минимальна.

Теорема 2.3.1 доказана. Она является теоретическим обоснованием остовного алгоритма оптимальной маршрутизации.

Пример работы этого алгоритма приведен на рис.2.3.4., где остов с минимальной стоимостью выделен жирными линиями.

Рис. 2.3.4. Пример симметричного графа ТКС с построенным в нем остовом минимальной стоимости.