 |
Много-адресная маршрутизация в динамических ТКС
|
|
|
|
В современных ТКС существует три типа маршрутизации:
- одно-адресная (unicast)
- много-адресная (multicast)
- широковещательная (broadcast)
Одно-адресная маршрутизация связывает один узел-источник и один узел-получатель ТКС. Многоадресная маршрутизация связывает один узел-источник и несколько узлов-получателей (или один узел-получатель и несколько узлов-источников ТКС.
При широковещательной маршрутизации пакеты данных передаются от одного узла-источника ко всем остальным узлам ТКС.
Много-адресная маршрутизация с одним узлом-получателем и несколькими узлами-источниками может рассматриваться как одна из разновидностей одно-адресной маршрутизации, при которой от каждого узла-источника строится свой оптимальный маршрут. Такой подход применим в силу того, что содержимое передаваемых пакетов данных может быть своим для каждого узла-источника. Поэтому пакеты данных, передаваемые с этих узлов, могут рассматриваться как самостоятельные потоки в этом случае совокупность локально-оптимальных маршрутов, независимо определяемых каждым узлом-источником, соответствует глобально-оптимальному решению задачи маршрутизации для всей группы узлов с заданными IP-адресами.
Особенность много-адресной маршрутизации в случае одного узла-источника и группы узлов-получателей ТКС состоит в том, что потоки данных, принимаемых узлами-получателями, будут одинаковыми. Поэтому графовым аналогом решения задачи будет дерево оптимальных маршрутов от узла-источника к группе узлов-получателей, причем интенсивности потоков данных на всех каналах связи, соответствующих ребрам этого дерева, будут равными (считается, что каналы связи обладают неограниченной пропускной способностью).
|
|
|
Таким образом, при геометрической трактовке данной задачи, интенсивности потоков данных роли не играют. Поэтому их можно исключить из рассмотрения.
Формализация данной задачи маршрутизации заключается в следующем.
Пусть ТКС соответствует граф G(A,R,W).
Тогда узлу-источнику будет соответствовать некоторая вершина 
, а группе узлов-получателей – другие вершины графа 
Требуется построить дерево оптимальных (кратчайших) маршрутов Tопт, такое, что стоимость любого маршрута вида
, (3.5.1)
входящего в Tопт, будет минимальной из всех возможных маршрутов из s в fi.
Таким образом, решением данной задачи оптимальной много-адресной маршрутизации будет поддерево дерева оптимальных (кратчайших) маршрутов, построенное от узла-источника к остальным узлам– получателям ТКС.
Модифицируем алгоритм Дейкстры для задачи много-адресной маршрутизации. Пусть узел-источник s0 и множество групп узлов-получателей 
зафиксированы. Тогда задача много-адресной маршрутизации будет состоять в построении дерева оптимальных (кратчайших) маршрутов от узла-источника s0 ко всем узлам из групп узлов-получателей 
и в определении на каждом узле дерева распределения потока для каждой группы узлов-получателей ТКС. Не умаляя общности, будем считать, что узлами-получателями из множества групп Ψ будут все узлы ТКС, кроме узла s0, т.е. F =(A \ s0).
Опишем работу алгоритма много-адресной маршрутизации. Введём следующие обозначения:
– множество соседних ai узлов ТКС;
– множество узлов, обработанных алгоритмом;
(
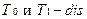)– множество узлов, обрабатываемых алгоритмом;
–остальные узлы ТКС;
– стоимость ребра 
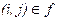, причём
w(i,j) =0; 
, если эти два узла не соединены непосредственно,
, если эти два узла непосредственно соединены;
L(j), 
- это оценка алгоритмом стоимости маршрута от узла-источника s0 до узла v; если 
, то это стоимость кратчайшего маршрута от s0 до v. Для остальных j это значение не определено.
|
|
|
Требуется построить дерево оптимальных (кратчайших) маршрутов от узла-источника s0 до остальных узлов и вычислить их стоимости, а также для каждого узла 
и группы узлов-получателей F определить множество 
, соответствующее распределению потока от s0 к F через узел ai.
Работа алгоритма заключается в следующем:
Инициализация
T1 - пусто, T1 ={ s0 }, т.е. вначале множество обработанных узлов состоит только из узла-источника. Узлу-источнику сопоставляется пустой маршрут.
L (v)= w(s0,v) для 
, т.е. начальные стоимости маршрутов к соседним узлам – это веса соответствующих ребер графа G, причём L(s0)=0.
Все 
пусты.
Шаг алгоритма
Берем из T1 узел с минимальной оценкой стоимости маршрута и помещаем его в T0 , и обозначаем соответствующий ему маршрут как оптимальный (кратчайший). Иными словами, находим 
такой, что
. (3.5.2)
При этом рассматриваем все ребра с начальным узлом x. Для каждого ребра (x, j) выполняется одно из трех действий:
А) если , то никаких действий не производится;
Б) если 
, то j переводится из множества T2 в T1, причем ей сопоставляются значение
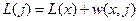, (3.5.3)
а также маршрут, состоящий из кратчайшего маршрута до x и ребра (x,j).
В) если , то производится новая оценка
, (3.5.4)
и узлу j сопоставляется соответствующий оценке маршрут (либо прежний, либо как в Б)).
Для каждого узла ai, составляющего полученный оптимальный (кратчайший) маршрут, кроме узла x, и всех групп узлов-получателей F, содержащих x, добавляем в узел aj, такой, что ребро (ai,aj) входит в оптимальный (кратчайший до x) маршрут.
Итерации алгоритма повторяются до тех пор, пока T0 не станет равно s. По окончании работы алгоритма для каждого узла x будет определен оптимальный (кратчайший) маршрут к нему от узла-источника, а значение L(x), вычисленное согласно (3.5.4) будет соответствовать стоимости этого маршрута.
|
|
|
