Матричные модели ТКС и их взаимосвязь

При оценке коммуникационных возможностей ТКС удобно использовать матричные представления ТКС. Матричной моделью ТКС будем называть коммуникационную матрицу C размерности N´N со следующими двоичными компонентами

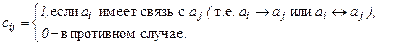(1.6.2.1)

Заметим, что для коммуникационных матриц любых ТКС с односторонними или двухсторонними связями справедливы соотношения

(1.6.2.2)

отражающие недопустимость связей вида (1.6.1.4). Соотношения (1.6.1.6) означают, что диагональные элементы всех коммуникационных матриц равны 0.

Важно отметить, что любая двоичная (бинарная) матрица, все элементы главной диагонали которой равны 0, является коммуникационной матрицей некоторой ТКС. По этой матрице можно построить графовую модель (коммуникационный граф) ТКС.

По графовой модели ТКС с произвольными (смешанными) связями можно однозначно построить матричную модель ТКС, т.е. коммуникационную матрицу, и наоборот. Например, для графовых моделей ТКС, изображенных на рис. 1.6.1 a),b) и c), соответствующие матричные модели имеют вид

(1.6.2.3)

В случае ТКС с односторонними связями (в отличие от ТКС с двусторонними связями) коммуникационная матрица имеет особенности, связанные с доминированием одних узлов ТКС над другими. Поэтому будем называть её коммуникационной матрицей ТКС с односторонними связями.

Компоненты этой двоичной (бинарной) матрицы размерности N´N для ТКС с односторонними связями определяются по формулам

(1.6.2.4)

. (1.6.2.5)

Отсюда следует, что тогда и только тогда, когда при i¹ j. Это означает, что если некоторый элемент , то симметричный ему (относительно нулевой главной диагонали матрицы ) элемент , и наоборот. Поэтому элементы , стоящие в i -ой строке матрицы

, соответствует только тем узлам ТКС, над которыми доминирует узел a_i, а единичные элементы, стоящие в j -ом столбце, соответствуют тем узлам ТКС, которые доминируют над a_{i .}

На рис. 1.6.2. представлен пример графовой и матричной модели для ТКС с односторонними связями.

Анализ графовых и матричных моделей ТКС позволяет ответить на многие вопросы, связанные с проектированием, управлением и использованием ТКС. Среди множества таких вопросов отметим следующие:

- со сколькими узлами ТКС непосредственно (через рёбра графа- каналы связи) или косвенно (через допустимые пути на графе ТКС) связан каждый узел?

- сколькими путями (маршрутами) каждый узел ТКС связан с любым другим узлом через один, два и т.д. промежуточных узлов?

- может ли каждый узел ТКС быть связан непосредственно или косвенно с любым другим узлом?

	a1	a2	a3	a4
a1
a2
a3
a4

 

 

Рис. 1.6.2. Графовая и матричная модели ТКС с односторонними связями

 

- каким образом следует изменить структуру (топологию связей) ТКС, чтобы расширить её телекоммуникационные возможности до требуемого уровня?

Графовой модели ТКС, имеющей N узлов и М рёбер (каналов связей) можно сопоставить матрицу инциденций E размерности N´M, столбцы и строки которой соответствуют узлам и рёбрам графа. Элементы этой матрицы определяются по формулам

(1.6.2.6)

Матрица инциденций характеризует некоторые важные свойства графа ТКС. Например, поскольку ребро графа инцидентно только двум вершинам графа, то каждый столбец матрицы Е= | e_ij | содержит ровно два единичных элемента.

Каждой подсети ТКС, рассматриваемой как его компонента (подграф), соответствует подматрица E_k матрицы инциденций E. При соответствующей нумерации узлов и рёбер внутри каждой k-ой компоненты и между всеми компонентами матрицу E всегда можно представить в блочно-диагональной форме.

Матрица инциденций E обеспечивает полное описание графа (графовой модели) ТКС.

Для ориентированных и неориентированных графов ТКС с односторонними или двусторонними связями можно определить матрицу смежности узлов Q размерности N´N. Элементы q_ij этой матрицы на пересечении i -ой строки и j -ого столбца определяются как число рёбер (односторонних или двусторонних связей), ориентированных от узла i к узлу j (в случае односторонних связей) или инцидентных одновременно i -ому и j -ому узлу ТКС (в случае двусторонних связей). Если q_ij = 0, то это означает, что i -ый и j -ый узел не связаны рёбром.

Степени матрицы смежности Q¹,Q²,…,Q^k несут важную информацию о существовании 2-, 3-, …, k-звенных маршрутов между любыми узлами ориентированного графа ТКС с односторонними связями, а именно: элементы матрицы Q^k равны числу ориентированных k-звенных маршрутов между соответствующими узлами ТКС.

Таким образом, для ТКС с ориентированными связями каждый узел достижим из любого другого узла ориентированным маршрутом, состоящим из k рёбер (односторонних связей).

По графу ТКС, узлы которого перенумерованы, можно построить матрицу маршрутов (коммуникационных путей) Р. Строки этой матрицы соответствуют ориентированным маршрутам из первого узла a₁ в последний a_N, а столбцы - рёбрам графа ТКС. При этом элементы p_ij матрицы маршрутов P принимают значение 1 или 0 в зависимости от того, принадлежат ли данное ребро графа данному маршруту или нет.

 

1.6.3. Критерии коммуникабельности ТКС

Важнейшей характеристикой управляемой глобальной ТКС является её производительность. Реальная производительность ТКС существенно зависит от используемой системы управления и может приближаться к определённому пределу, который естественно назвать потенциальной производительностью ТКС.

Производительность глобальных ТКС характеризуется следующими основными показателями:

- время реакции ТКС,

- пропускная способность ТКС,

- задержка передачи потоков данных.

Время реакции ТКС - это длительность T интервала времени между начальным моментом t₀ запроса пользователя к ТКС и конечным моментом t_T получения ответа на этот запрос, т.е.

T=t_T-t₀. (1.6.3.1)

Значение этого показателя T=T(a₁, a₂, …) зависит от ряда факторов:

a₁ - тип службы ТКС, к которой обращается пользователь;

a₂ - тип узлового сервера, к которому обращается пользователь;

a₃ - текущее состояние элементов ТКС (загруженность сегментов, маршрутизаторов и коммутаторов, через которые проходит запрос, и т.п.);

a₄ - время дня, в которое пользователь обращается с запросом в ТК, и т. п.

Время реакции ТКС является глобальной характеристикой производительности ТКС с точки зрения пользователя. Оно определяется по формуле

(1.6.3.2)

где T₁ - время подготовки запроса на компьютере пользователя, T₂ - время передачи запроса между пользователем (клиентом) и узловым сервером ТКС через коммуникационное оборудование и сегменты ТКС, T₃ -время обработки запроса на сервере ТКС; T₄ - время передачи ответов от сервера к пользователю (клиенту); T₅ - время обработки полученного ответа на компьютере пользователя (клиента).

Представленное аддитивное разложение времени реакции T на составляющие T_i не интересует пользователя. Ему важен конечный результат - минимальное значение времени реакции глобальной ТКС на его запрос.

Знание сетевых локальных составляющих T_i времени реакции T позволяет оценить производительность отдельных элементов ТКС, выявить наиболее непроизводительные элементы ТКС и минимизировать глобальное время реакции T средствами управления или путём модернизации используемого оборудования ТКС.

Таким образом, открывается принципиальная возможность повышения производительности ТКС за счёт оптимизации (по быстродействию) управления. Например, можно минимизировать T₃ за счёт управляемого выбора кратчайших или быстрейших маршрутов “клиент-сервер”, удовлетворяющих информационный запрос пользователя. Для этого можно использовать нейросетевые модели оптимальных маршрутизаторов.

Пропускная способность ТКС V - это объём потока данных, переданных ТКС или её компонентами за единицу времени. Обычно величина V изменяется в битах в секунду или в пакетах в секунду.

В отличие от времени реакции ТКС, зависящего, в частности, от пользователя, пропускная способность ТКС V является объективным показателем производительности сети, характеризующим скорость передачи потоков данных между узлами ТКС через различное коммуникационное оборудование. Принято различать среднюю, мгновенную и максимальную пропускную способность ТКС.

Средняя пропускная способность ТКС V_* определяется как объём потока данных, переданный за достаточно большое время (например, за час, день или неделю).

Мгновенная пропускная способность ТКС V₀ - это объём потока данных, переданных за достаточно малое время (например, за 1 мс или 1 с).

Максимальная пропускная способность V_max определяется как наибольшее значение величины V₀, зафиксированная на всём интервале наблюдения за работой ТКС.

Среди этих показателей пропускной способности ТКС или её компонентов наиболее информативными являются величины V_* и V_max. Средняя пропускная способность V_* оценивает производительность ТКС на достаточно большом интервале времени, когда непредсказуемые ими случайные “пики” и “спады” трафика в какой-то мере компенсируют друг друга. Максимальная пропускная способность V_max характеризует работоспособность ТКС при “пиках” трафика (например, в начале рабочего дня, когда многие пользователи одновременно регистрируются и обращаются с запросами в ТКС).

Глобальная пропускная способность ТКС V зависит от локальных пропускных способностей V_j её компонент, измеряемых, например, между узлами сети или входным и выходным портами маршрутизатора. Вследствие последовательного характера передачи потоков данных различными компонентами ТКС глобальная пропускная способность любого сложного маршрута движения данных в ТКС будет равна минимальной из пропускных способностей элементов этого маршрута, т.е.

(1.6.3.3)

Поэтому для повышения глобальной пропускной способности ТКС необходимо повысить пропускную способность её самых медленных компонент. Это можно сделать, в частности, средствами управления ТКС (например, путём оптимизации маршрутизаторов) по критерию поиска кратчайших или быстрейших коммуникационных маршрутов.

Производительность глобальной ТКС снижается из-за неизбежной задержки передачи информации по сетевым каналам и устройствам. Величина задержки D определяется как разность между моментом t₁ появлния пакета на выходе и моментом t₀ его поступления на вход соответствующего сетевого устройства, т.е.

D= t₁ - t₀ . (1.6.3.4)

Этот показатель обычно лежит в пределах 100 мс - 10 с. Он отличается от времени реакции ТКС тем, что не учитывает задержки обработки информации в каналах связи ТКС. Задержка передачи не зависит от пропускной способности ТКС. В частности, канал связи через геостационарный спутник имеет задержку передачи D ³ 0,2 с, хотя его пропускная способность очень высока (например, 2 Мбит/c).

Рассмотрим матричную модель ТКС с односторонними связями в форме коммуникационной матрицы . Поскольку эта бинарная матрица квадратная, можно вычислить её степени , и т.д., а также сформировать сумму таких матриц в виде коммуникационного матричного полинома.

(1.6.3.5)

Компоненты матрицы вычисляются по формуле

, (1.6.3.6)

причём слагаемые вида в (1.6.3.6) не равны 0 только в том случае, когда не равны 0 оба сомножителя, т.е. когда .

Заметим, что если , то узел a_i имеет доминирующую связь с узлом a_k. Аналогично, если , то узел a_k имеет доминирующую связь над узлом a_j. Иначе говоря, в ТКС с односторонними (доминирующими) связями имеют место соотношения

a_i ® a_k, a_k ® a_j. (1.6.3.7)

Соотношение доминирования вида

a_i ® a_j,i¹ j, (1.6.3.8)

будем называть однозвенным доминированием узла a_i над узлом a_j или однозвенным маршрутом между узлами a_i и a_{j .}

Соотношения вида (1.6.3.7) назовём двузвенным доминированием узла a_i над узлом a_j или двузвенным маршрутом между узлами a_i, a_k и a_{j .}

Аналогичным образом определяются понятия о k-звенном доминировании или маршруте при k=3,4,…,N.

Очевидно, что число двузвенных доминирований (маршрутов) узла a_i над узлом a_j

равно . Поэтому это число можно вычислить по формуле (1.6.3.6).

Для матричной модели ТКС с односторонними связями, изображённой на рис. 1.6.2, вычислим следующие матрицы

(1.6.3.9)

Анализ этих матриц показывает, что узел a₁ имеет однозвенное доминирование (маршрут) над узлами a₂ и a₄ и два двузвенных доминирования (маршрута) над узлом a₃ . Аналогично узлы a₃ , a₂ и a₄ имеют однозвенное доминирование над узлами a₁ , a₂ и a₄ .

В целом можно утверждать, что узлы a₁ , a₂ и a₄ (но не узел a₂) могут доминировать (т.е. иметь одно- или двузвенный маршрут) над каждым из остальных узлов ТКС и каждый из узлов a₁ , a₂ и a₃ одно- или двузвенно доминирует над каждым из остальных узлов ТКС. В то же время узел a₄ не может доминировать подобным образом над узлом a₂.

Для анализа k-звенных доминирований и маршрутов в ТКС при k>2 вычислим матрицы и . Тогда элементы i -ой строки матрицы определяют k-звенные доминирования (маршруты) для узла a_i, а сумма этих элементов даёт число всех k-звенных доминирований (маршрутов), реализуемых узлом a_i.

Аналогично элементы i -ой строки матрицы дают число 1-, 2-…, k-звенных доминирований (маршрутов) для узла a_i, а сумма элементов i -ой строки определяет число всех таких доминирований (k-звенных маршрутов) для узла a_i.

Для матричного анализа коммуникационных возможностей ТКС с односторонними связями полезно ввести понятие k-звенного веса узла, где k=1,2…,N.

Будем называть 2-звенным коммуникационным весом узла a_i ТКС число всех однозвенных и двузвенных маршрутов соединения (доминирования), которые этот узел может иметь с другими узлами ТКС.

Очевидно, что 1-звенный вес узла a_i для всех однозвенных маршрутов равен сумме компонент i -ой строки коммуникационной матрицы , т.е.

. (1.6.3.10)

Аналогично, вес узла для всех двузвенных маршрутах равен сумме компонент i -ой матрицы , т.е.

(1.6.3.11)

Таким образом, 2-звенный коммуникационный вес узла a_i ТКС определяется по формуле

. (1.6.3.12)

Этот вес равен сумме компонентов i -ой строки матрицы .

Для примера вычислим веса (1.6.3.12) узлов ТКС, графовая и матричная модели которых представлены на рис. 1.6.2. Тогда получим

(1.6.3.13)

Аналогичным образом, можно определить k-звенный вес узла a_i ТКС при k³3. В случае k=N этот N-звенный вес, определяющий возможность N-звенных маршрутов, будет равен сумме компонент i- ой строки матрицы S^(N) вида (1.6.3.5).

В общем случае между узлами ТКС могут существовать как односторонние, так и двусторонние связи. Такие ТКС будем называть ТКС с произвольными (смешанными) связями. В этом случае узлы ТКС могут иметь все виды связей типа (1.6.1.2) и (1.6.1.3).

Рассмотрим ТКС со смешанными связями. В этом общем случае матричная модель ТКС со смешанными связями задаётся коммуникационной матрицей C (1.6.2.4), (1.6.2.5).

Допустимые связи между узлами ТКС имеют вид (1.6.1.2) или (1.6.1.3). На языке коммуникационных матриц это означает, что справедливы соотношения (1.6.1.3), т.е. все компоненты главной диагонали матрицы C равны 0. Наличие 1 на пересечении i -ой строки и j - го столбца коммуникационной матрицы C означает, что между узлами a_i и a_j ТКС имеется связь одного из допустимых типов (1.6.1.2) или (1.6.1.3).

Для анализа коммуникационных возможностей ТКС с произвольными (смешанными) связями вычислим степени матрицы C и их сумму, т.е. коммуникационный матричный полином вида

(1.6.3.14)

Вычислим компоненты матрицы C² по формуле

. (1.6.3.15)

Тогда её компонента (1.6.3.15) будет равна числу двузвенных связей (маршрутов), соединяющих узел a_i с узлом a_j ТКС.

Для примеров ТКС со смешанными связями, представленных своими графовыми моделями на рис. 1.6.1, a,b,c, и матричными моделями (1.6.1.7), получим соответственно

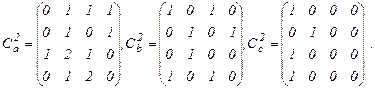(1.6.3.16)

Вычисляя суммы вида S⁽²⁾=C+C², получим

(1.6.3.17)

Анализируя, например, матрицу , заключаем, что узел a₁ может общаться сам собой, используя двузвенную связь вида

a₁ ®a₂ ®a₁.

Узел a₄ имеет только двузвеные связи с узлами a₁ и a₃ вида

a₁ ®a₂ ®a₁, a₄ ®a₂ ®a₃

и не имеет однозвенных связей (маршрутов).

Вычисляя матрицы и определяя их элементы , принадлежащие i -ой строке и j - му столбцу, получим число 3-, 4-, …, N-звенных маршрутов, связывающих узлы a_i и a_j ТКС.

Рассмотрим ТКС из N узлов со смешанными связями, имеющую полносвязную топологию. В этом случае между любыми двумя узлами ТКС существуют односторонние или двухсторонние связи вида (1.6.1.2) или (1.6.1.3) и не существует связей вида (1.6.1.4).

Возникает вопрос: существует ли в этой ТКС по крайней мере один узел, который связан с каждым из остальных узлов ТКС однозвенным или двузвенным маршрутом? Положительный ответ на этот вопрос означает, что в ТКС с полносвязной топологией имеется один или несколько узлов, которые могут послать каждому другому узлу ТКС или получить от каждого другого узла ТКС однозвенное или двузвенное сообщение.

Теорема 1.6.3.1. Предположим, что ТКС имеет полносвязную топологию и состоит из N узлов c произвольными (смешанными) связями. Тогда существует по крайней мере один узел ТКС, который может

1) послать любому другому узлу ТКС однозвенное или двузвенное сообщение, т.е. между ними существует одно- или двузвенный маршрут;

2) получить от любого другого узла ТКС однозвенное или двузвенное сообщение, т.е. между ними существует одно- или двузвенный маршрут.

Сначала докажем первое утверждение теоремы с помощью следующей леммы.

Лемма 1.6.3.1. Если узел a₁ не может послать однозвенное или двузвенное сообщение каждому из остальных узлов ТКС, т.е. a₂, a₃, …., a_N, то число узлов ТКС, которыми узел a_i,i¹ j, может послать однозвенное сообщение, по меньшей мере на 1 больше числа узлов ТКС, которым узел a_i,i¹ j, может послать однозвенное сообщение.

Для доказательства этой леммы заметим, что из условия теоремы 1.6.3.1 следует, что

(i) если узел a₁ не может послать узлу a_i,i¹ j однозвенное сообщение (т.е. если неверно, что a₁ ®a_i), то

a_i ®a₁,(1.6.3.18)

(ii) если узел a₁ не может послать узлу a_i,i¹ j двузвенное сообщение (т.е. если для всех k неверно, что a₁ ®a_k ®a_i), то из a₁ ®a_k следует также, что

(iii) a_i ®a_k. (1.6.3.19)

Действительно, если a₁ ®a_k, то неверно, что a_k®a_i. Тогда ввиду полносвязности ТКС (по условиям теоремы 1.6.3.1) справедливо соотношение (1.6.3.19), т.е. узел a_i доминирует над узлом a_k.

Согласно утверждению (ii), если узел a₁ может передать однозвенное сообщение какому-нибудь другому узлу a_k ТКС, то тому же узлу a_k может передать однозвенное сообщение также и узел a_i,i¹ 1, i¹k. C учётом условия (i) отсюда следует, что узел a_i может передать по крайней мере на одно однозвенное сообщение больше, чем узел a₁.

Используем лемму 1.6.3.1 для доказательства теоремы 1.6.3.1. Пусть

. (1.6.3.20)

Назовём r_i рангом i -ой строки коммуникационной матрицы C для полносвязной ТКС. Предположим, что ранг r₁ является максимальным среди оcтальных рангов (1.6.3.20) (Этого всегда можно добиться соответствующим переименованием узлов a₁, a₂, …., a_N ТКС).

Докажем, что в этом случае для узла a₁ справедливо первое утверждение теоремы 1.6.3.1. Предположим противное. Тогда существует узел a_i, i >1, которому a₁ не может передать однозвенное или двузвенное сообщение. В этом случае, число узлов ТКС, которым узел a_i может передать однозвенное сообщение, по крайней мере на 1.6.3.1 больше числа узлов ТКС, которым узел a₁ может передать однозвенное сообщение. Отсюда следует, что r_i > r₁. Но это противоречит предположению о том, что

. (1.6.3.21)

Полученное противоречие завершает доказательство утверждения теоремы 1.6.3.1.

Аналогичным образом доказывается второе утверждение теоремы 1.6.3.1.

Теорему 1.6.3.1 можно переформулировать на языке коммуникационных матриц ТКС.

Теорема 1.6.3.2. Пусть С - коммуникационная матрица ТКС с полносвязной топологией, состоящей из N узлов с произвольными (смешанными) связями. Тогда в матрице

S⁽²⁾ = C + C² (1.6.3.22)

существует

1) хотя бы одна строка, все элементы которой (за исключением элементов на главной диагонали) больше 0, т.е.

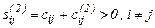(1.6.3.23)

2) хотя бы один столбец, все элементы которого обладают свойством (1.6.3.23).

Следствие. В условиях теоремы 1.6.3.2 справедливы следующие утверждения:

1) узел ТКС, который имеет максимальную сумму элементов строки коммуникационной матрицы С, может передавать однозвенные или двузвенные сообщения каждому из остальных узлов ТКС, т.е. между этими узлами существует одно- или двузвенный маршрут;

2) узел ТКС, который имеет максимальную сумму элементов столбца коммуникационной матрицы С, может получить однозвенные или двузвенные сообщения от каждого из остальных узлов ТКС.

Рассмотрим ТКС с N узлами, имеющими только односторонние связи вида (1.6.1.2) и исследуем их коммуникабельность с доминированием в классе одно- и двузвенных сообщений (маршрутов).

Теорема 1.6.3.3. Предположим, что ТКС имеет N узлов с односторонними связями. Тогда существует по крайней мере один узел

(i) который может однозвенно или двузвенно доминировать над каждым из остальных узлов ТКС, т.е. существуют исходящие из этого узла одно- или двузвенные маршруты, ведущие к другим узлам;

(ii) над которым однозвенно или двузвенно доминирует каждый из остальных узлов, т.е. существуют одно- и двузвенные входящие в узел маршруты, начинающиеся в других узлах ТКС.

Эту теорему можно переформулировать в терминах коммуникационных матриц для ТКС с односторонними связями.

Теорема 1.6.3.4. Пусть - коммуникационная матрица ТКС, состоящей из N узлов с односторнними связями. Тогда в матрице существует по крайней мере одна строка (а также столбец), все элементы которой (за исключением элемента на главной диагонали) отличны от 0, т.е.

Теоремы 1.6.3.3 и 1.6.3.4 являются следствием теорем 1.6.3.1 и 1.6.3.2 соответственно и относятся к ТКС, имеющим только односторонние связи.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: